Майкл Шермер - Магия чисел. Ментальные вычисления в уме и другие математические фокусы

1. Посмотрите на величину сотен (цифры, предшествующие последним двум) в данном примере.

2. Так как 75 находится между 8 2(8 х 8 = 64) и 9 2(9 х 9 = 81), то нам известно, что квадратный корень будет где-то в диапазоне «80 плюс». Следовательно, его первая цифра 8.

Существует два числа, квадраты которых заканчиваются на 9: 3 2= 9, 7 2= 49. Поэтому последняя цифра квадратного корня должна равняться 3 или 7. Таким образом, квадратный корень равен либо 83, либо 87. Какой из них?

3. Сравните исходное число с квадратом числа 85 (который можно легко посчитать как 80 х 90 + 25 = 7225). Так как 7569 больше, чем 7225, квадратный корень будет бóльшим числом, то есть 87.

Решим еще один пример.

Чему равен квадратный корень из 4761 ?

Поскольку 47 лежит между 6 2= 36 и 7 2= 49, ответ должен находиться в диапазоне «60 плюс». Если последняя цифра квадрата равна 1, то последняя цифра квадратного корня должна быть 1 или 9. Так как 4761 больше 65 2= 4225, то квадратный корень должен равняться 69. Как и с предыдущим трюком для кубического корня, этот метод можно использовать только тогда, когда исходное число является полным квадратом.

Следующий трюк мне впервые показал Джеймс Рэнди, который эффективно использовал его в своей магии. В нем волшебник предсказывает сумму четырех случайно выбранных трехзначных чисел.

Чтобы подготовить такой фокус, понадобятся три колоды из девяти карт каждая и лист бумаги с записанным числом 2247, который вы запечатаете в конверт. Далее над каждым комплектом карт произведите следующие действия.

На колоде А запишите такие цифры (одно на каждую карту):

4286 5771 9083 6518 2396 6860 2909 5546 8174

На колоде Б запишите числа:

5792 6881 7547 3299 7187 6557 7097 5288 6548

На колоде В запишите следующие числа:

2708 5435 6812 7343 1286 5237 6470 8234 5129

Выберите троих человек из аудитории и вручите им по колоде карт. Пусть каждый из них наугад вытащит оттуда одну карту. Допустим, это карты с числами 4286, 5792 и 5435. Теперь, соблюдая очередность, пусть каждый громко назовет одну из цифр четырехзначного числа: сначала человек А , потом человек Б и, наконец, человек В . Скажем, они назвали цифры 8, 9 и 5. Запишите их (получится число 895) и скажите: «Вы должны признать, что данное число — результат абсолютно случайного выбора и его нельзя заранее предсказать».

Далее пусть три человека назовут другие цифры своих карт. Скажем, 4, 5 и 3. Запишите 453 ниже числа 895. Затем повторите данную процедуру еще два раза для двух оставшихся чисел, получив в итоге четыре трехзначных числа, например:

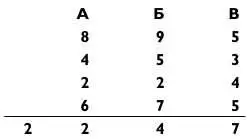
Затем пусть кто-нибудь сложит эти четыре числа и назовет сумму. А дальше пусть кто-то откроет конверт и покажет ваше предсказание. Теперь наслаждайтесь аплодисментами!

Почему это работает

Взгляните на числа на картах каждой колоды и подумайте, прослеживается ли в них какая-либо последовательность. Каждый набор чисел в сумме дает одинаковую величину. Сумма цифр каждого числа колоды А равна 20. Сумма цифр каждого числа колоды Б — 23. И сумма цифр каждого числа колоды В равна 17. Поскольку цифры из колоды В, которые в правом столбике, всегда в сумме дают 17, то в итоговой сумме в разряде единиц можно записать 7 и запомнить перенос 1 в следующий разряд.

Так как цифры из колоды Б в сумме дают 23, то в итоговой сумме в разряде десятков можно записать 4 (3 + 1) и запомнить перенос 2 в следующий разряд. Наконец, цифры из колоды А в сумме дают 20, поэтому после прибавления 2 получим итоговую сумму 2247!

Мы завершим нашу книгу одним из проверенных временем подвигов ментальных вычислений — определением дня недели, на который приходится чей-либо день рождения. Это действительно очень практический навык. Вряд ли вас каждый день кто-то будет просить возвести в квадрат трехзначное число, но почти ни один день не проходит без того, чтобы кто-то не упоминал дату из прошлого или будущего. Всего лишь немного практики, и вы сможете быстро и легко определять день недели практически любой исторической даты.

Сначала присвоим кодовый номер каждому дню недели.

Их легко запомнить.

Далее нам понадобится код для каждого месяца. Эти коды применимы для любого года за исключением високосных. Для високосного года (например, 2000, 2004, 2008 и т. д.) кодом для января будет 5, а для февраля — 1.

Теперь вычислим день недели для любой даты в 2006 году.

После этого опишем 2007 год, затем 2008-й и т. д., до конца вашей жизни. Когда все даты из будущего будут определены, мы заглянем в прошлое и вычислим дни недели для любой даты из 1900-х или любого другого века.

Каждому году присвоен кодовый номер, и в случае 2006 года таковым будет 0 (см. таблицу ниже).

Чтобы вычислить день недели, нужно просто сложить код месяца, день месяца (дата) и код года. Таким образом, для 3 декабря 2006 года рассчитываем

Код месяца + Дата + Код года = 4 + 3 + 0 = 7.

Следовательно, эта дата приходится на 7-й день недели, то есть воскресенье.

Что вы скажете о 18 ноября 2006 года? Поскольку код ноября — 2, имеем:

Код месяца + Дата + Код года = 2 + 18 + 0 = 20.

Так как дни недели повторяются каждые семь дней, нужно от ответа (20) отнять любое кратное 7 (то есть 7, 14, 21, 28, 35, .), и это никак не повлияет на номер дня недели. Итак, заключительное действие сводится к вычитанию из полученной суммы наибольшего кратного 7. В данном случае получаем 20–14 = 6. Следовательно, 18 ноября 2006 года приходится на субботу.

Что можно сказать о 2007 годе? Точнее, что происходит с вашим днем рождения при переходе от одного года к следующему? Большинство годов состоят из 365 дней, а так как 365 = 7 х 52 + 1, то день недели вашего рождения сдвинется на один день вперед. Если между вашими днями рождения 366 дней, то день недели вашего рождения сдвинется на два дня вперед. Поэтому для 2007 года мы вычисляем день недели как и раньше, но применяем код года, равный 1. Далее следует 2008 год — високосный. (Високосный год бывает раз в четыре года, так что 2000, 2004, 2008, 2012… 2096 — високосные годы XXI века.) Поэтому для 2008 года его код увеличивается на два и равен 3. Следующий 2009 год не високосный, поэтому код увеличивается на 1 (и равен 4).

Таким образом, для 2 мая 2007 года, например, имеем:

Код месяца + Дата + Код года = 0 + 2 + 1 = 3.

Следовательно, данная дата приходится на среду.

Для 9 сентября 2008 года имеем: