Борис Бирюков - Жар холодных числ и пафос бесстрастной логики

В рассуждении первого химика можно выделить следующие элементарные высказывания (суждения): «Нечто есть соль», «Нечто есть органическое тело» и «Нечто окрашено». Все рассуждение можно представить в виде следующего сложного условного суждения: «Если нечто есть соль и (это нечто) не окрашено, то (это нечто) есть соль и не есть органическое тело или есть органическое тело и не окрашено». Заменив элементарные высказывания соответственно переменными А1 A2 и A3, а вместо логических союзов «и», «или» и «если..., то» употребив знаки &, V и →, мы можем представить логическую форму этого сложного высказывания следующим выражением: ((А1 & ~A3) → ((A1 & ~A2) V (А2 & ~A3))). Для решения спора между двумя химиками надо определить, представляет ли оно тождественно-истинное высказывание.

Проведал соответствующие преобразования, на этот раз без объяснений (мы предоставляем читателю самостоятельно определить те схемы аксиом нашего исчисления, которым мы пользуемся на каждом шаге).

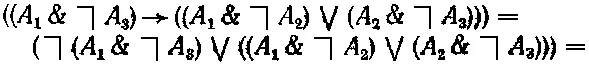
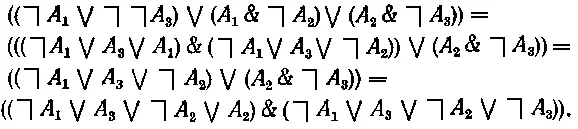
В полученной на последнем шаге двучленной конъюнкции в каждом члене (представляющем собой дизъюнкцию пропозициональных переменных или их отрицаний) имеется 5 обязательно какая-то переменная и ее отрицание. Следовательно, оба члена конъюнктивной формы тождественно-истинны и, значит, тождественно-истинна и она сама. Итак, рассуждение первого химика было логически правильным, а его оппонент допустил ошибку.

Обратим теперь внимание на то, что в обеих рассмотренных интерпретациях фигурировали множества элементов, являющихся областями значений пропозициональных переменных; именно на этих множествах получали определение операции ~, &, V, свойства которых были ранее установлены равенствами 1—17 из пункта IV, и в этих же множествах находились элементы — результаты применений операций (последнее свойство называется замкнутостью множества относительно данных операций). Тем самым эти множества составляют то, что называется булевыми алгебрами. Булева алгебра—это любое множеством объектов, для которых определены одна одночленная (одноместная, унарная) операция (~) и две двучленных (двуместных, бинарных) операции (&, V) причем множество М замкнуто относительно этих операций; в нем имеются объекты, соответствующие константам 0 и 1 рассмотренного нами исчисления (нуль и единица булевой алгебры); одночленная операция, которую мы назвали отрицанием, подчиняется закону снятия двойного отрицания, а двучленные операции, которые мы назвали конъюнкцией и дизъюнкцией, обе коммутативны, ассоциативны, дистрибутивны одна относительно другой, подчиняются законам поглощения и, вместе с отрицанием, законам Де Моргана, а также законам, в которых фигурируют 0 и 1 (законы 14—17) (ср. с. 55) [20] 52 20. Впрочем, операции булевой алгебры можно задавать указанием и других наборов их свойств. О булевых алгебрах см., например: И. М. Яглом. Алгебра Буля.— В сб.: «О некоторых вопросах современной математики и кибернетики». М., 1965. . В первой из наших интерпретаций булевой алгеброй является множество из двух элементов — 0 и 1, во второй — множество истинностных значений (впрочем, можно считать, что булевой алгеброй здесь было множество высказываний [21] 53 21. Напоминаем, что здесь высказывание понимается «классически», то есть как выражение либо истинное, либо ложное, но не то и другое вместе. . понимаемых, однако, так, что высказывания, имеющие одно и то же истинностное значение, не различаются) [22] 54 22. При другом подходе булевой алгеброй для логической интерпретации нашего аппарата можно считать множество форм высказываний (рассматриваемых с точностью до отождествления равносильных форм) вместе с заданными на них операциями ~, &. V - такая булева алгебра высказываний оказывается алгеброй Линденбаума — Тарского, о которой см.: Е. Расёва, Р. Сикорскии. Математика метаматематики. М., 1972, с. 282 и далее. ; как мы убедимся ниже, имеются и другие интерпретации булевой алгебры.

Формальный аппарат, изложенный в пп. I—IV (пункт V, как говорят, не расширяет его возможностей), можно понимать как теорию абстрактной булевой алгебры — булевой алгебры как любого множества объектов (носителя), взятого вместе с семейством операций. определенных на этом множестве, которое удовлетворяет всем требованиям данного аппарата, причем как теорию в узком смысле: как некоторое исчисление (равенств). Такую теорию следует отличать от теории булевых алгебр в широком смысле, в которой исследуются свойства приведенного формального аппарата (и аналогичных ему построений) и его интерпретации, формализации булевых алгебр средствами тех или иных логических систем, обобщения понятия булевой алгебры и т. д.

В логике исчислением обычно называют систему правил порождения объектов, допускающих осмысление (интерпретацию), и позволяющую выделять среди осмысленных объектов такие, которые в интерпретациях оказываются в каком-либо разумном смысле истинными суждениями. В рассмотренном нами исчислении объекты возникают в два этапа:

на первом с помощью пп. I и II порождаются формулы (и —с помощью п. V —их сокращения),

на втором (п. III) из формул строятся равенства. Далее среди возникших таким образом объектов происходит отбор тех из них, которые в интерпретациях оказываются верными, отбор равенств [23] 55 23. Заметим, что булеву алгебру можно сформулировать и на основе отношения ≤ (или ≥). См: X. Б. Карри. Основания математической логики. М., 1969. , истолковываемых как суждения о свойствах элементов соответствующей булевой алгебры, выраженные в терминах ~, & и V. Этот отбор задается постулатами (п. IV); он основан на процедуре порождения верных равенств посредстве м правил вывода [b], исходя из равенств, представляющих собой аксиомы (согласно списку схем аксиом [а]).

Проиллюстрируем механизм подобного порождения на приведенном выше (с. 64) примере доказательства равенства

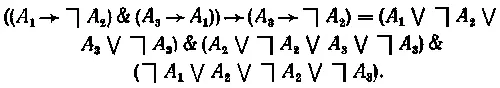
Шаг (1) состоял в следующем. Было взято равенство (A1 → ~A2) = (~A1 V ~A2), верное по определению (п. V), и к нему применено правило вывода —замена равным [b] следующим образом: в ((A1 → ~A2) & (A3 → A1)) →

(A3 → ~A2) часть (A1 → ~A2) была заменена на формулу (~A1 V ~A2), в результате чего получилось верное равенство:

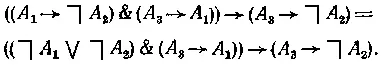
Здесь роль α, фигурирующей в формулировке правила замены равным, играло выражение (A1 → ~A2)» роль β — формула (~A1 V ~A2), роль Ф[а]—выражение ((А1 → A2) & (A3 → A1)) → ( A3 → ~A2). роль Ф[β] - выражение ((~A1 V ~A2) & (A3 → A1)) → (A3→ ~A2). На шагах (2) и (3) в последнем выражении была произведена аналогичная замена импликативных выражений равными им (в силу определения п. V) дизъюнктивными формулами. Читатель может самостоятельно проследить, как применялось правило замены (и правила, выражающие симметричность и транзитивность равенства) на всех шагах доказательства, приведенного на с. 64—65. Заметим, что на некоторых шагах правило замены использовалось несколько раз.