Жуан Гомес - Мир математики. т.2. Математики, шпионы и хакеры. Кодирование и криптография

3. Если окончательная сумма кратна 10 (то есть ее значение равно нулю по модулю 10), номер карты является действительным. Заметим, что именно последняя контрольная цифра делает общую сумму кратной 10.

* * *

DINER’S CLUB

Одной из первых кредитных карт, получивших широкое признание, была карта Diner's Club. Автором идеи был американец Фрэнк Макнамара. В 1950 г. ему удалось убедить различные рестораны принимать оплату безналично с помощью персональных гарантированных кредитных карт, которые Макнамара распространил среди своих лучших клиентов. Наиболее часто в первые десятилетия кредитными картами расплачивались за обеды американские коммивояжеры, будучи в дороге.

* * *

Например, пусть карта имеет следующий номер:

1234 5678 9012 3452

По алгоритму Луна имеем:

1∙2 = 2

3∙2 = 6

5∙2 = 10 => 1 + 0 = 1

7∙2=14 => 1 + 4 = 5 (или 14-9 = 5)

9∙2 = 18 => 1 + 8 = 9

1∙2 = 2

3∙2 = 6

5∙2 = 10 => 1 + 0 = 1

Далее найдем сумму результатов и цифр на четных позициях:

2 + 6 + 1 + 5 + 9 + 2 + 6 + 1 = 32

2 + 4 + 6 + 8 + 0 + 2 + 4 + 2 = 28

32 + 28 = 60

Результат равен 60, это число кратно 10. Поэтому номер карты является действительным.

Алгоритм Луна можно применить другим способом: номер карты ABCD EFGH IJKL MNOP является правильным, если удвоенная сумма цифр на нечетных позициях и сумма цифр на четных позициях плюс количество цифр на нечетных позициях, которые больше, чем 4, кратно 10. Это правило записывается так:

2 (A + C + E + G + 1 + К + М + О) + (B + D + F + H + J + L + N + P) + (количество цифр на нечетных позициях, которые больше, чем 4) = 0 (mod 10).

Применим это правило к предыдущему примеру:

1234 5678 9012 3452

2 (1 + 3 + 5 + 7 + 9 + 1 + 3 + 5) + (2 + 4 + 6 + 8 + 0 + 2 + 4 + 2) + (4) = 100 0 (mod 10).

Снова мы убедились, что номер кредитной карты является действительным, и показали, что на первый взгляд случайные номера карт соответствуют строгому математическому стандарту.

* * *

ПРИМЕР РАСЧЕТА КОНТРОЛЬНОЙ ЦИФРЫ КРЕДИТНОЙ КАРТЫ В EXCEL

Номер кредитной карты состоит из 15 цифр плюс контрольная цифра. Цифры сгруппированы в четыре группы по четыре цифры. Контрольная цифра (КЦ) рассчитывается следующим образом.

* * *

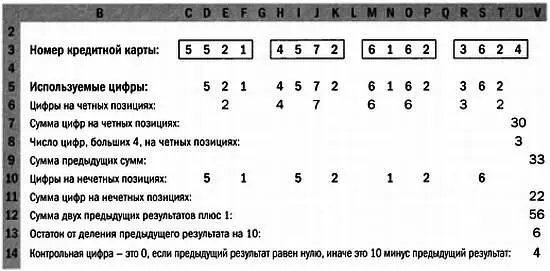
Можно ли восстановить цифру, отсутствующую в номере карты? Да, если мы имеем дело с действительной кредитной картой. Найдем, например, цифру X в номере 4539 4512 03X8 7356.

Начнем с умножения на 2 цифр на нечетных позициях (4–3—4—1–0—X—7–5), сразу преобразуя результат к одной цифре.

4∙2 = 8

3∙2 = 6

4∙2 = 8

1∙2 = 2

0∙2 = 0

X∙2 = 2Х

7∙2 = 14, 14 — 9 = 5

5∙2 = 10, 10 — 9 = 1.

Складывая цифры, стоящие на четных позициях, и новые цифры на нечетных, получим:

30 + 41+ 2Х = 71 + 2Х.

Мы знаем, что число (71 + 2Х) должно быть кратно 10.

Если значение X меньше или равно 4, то для таких X (71 + 2Х) никогда не будет кратно 10.

Если же значение X больше 4, то кратно 10 должно быть выражение (71 + 2Х + 1), так как X стоит на нечетной позиции. Видим, что выражение (72 + 2Х) кратно 10 только при X = 9.

Следовательно, мы нашли потерянную цифру 9, и полный номер кредитной карты: 4539451203987356.

Штрихкоды

Первая система штрихкодов была запатентована 7 октября 1952 г. американцами Норманом Вудландом и Бернардом Сильвером. Первые версии штрихкодов отличались от сегодняшних. Вместо привычных нам линий Вудланд и Сильвер придумали концентрические круги. Впервые штрихкоды начали официально использоваться в 1974 г. в магазине города Трой, штат Огайо.

Современные штрихкоды представляют собой последовательность черных полос (которые кодируются как 1 в двоичной системе) и пробелов между ними (которые кодируются как 0). Штрихкоды используются для идентификации физических объектов. Штрихкоды, как правило, печатаются на этикетках и считываются оптическими устройствами. Это устройства, похожие на сканер, которые измеряют отраженный свет и преобразуют темные и светлые области в буквенно-цифровой код, который затем посылается на компьютер. Существует множество стандартов для штрихкодов:

Толщина штрихов и пробелов в штрихкоде соответствует двоичным цифрам.

Code 128, Code 39, Codabar, EAN (этот стандарт появился в 1976 г. в двух версиях, состоящих из 8 и 13 цифр соответственно) и UPC (Universal Product Code — универсальный код товара, используемый в основном в США и доступный также в двух версиях из 12 и 8 цифр соответственно). Наиболее распространенной является 13-значная версия EAN. Несмотря на разнообразие стандартов, штрихкоды позволяют идентифицировать любой продукт в любой части мира быстро и без существенных ошибок.

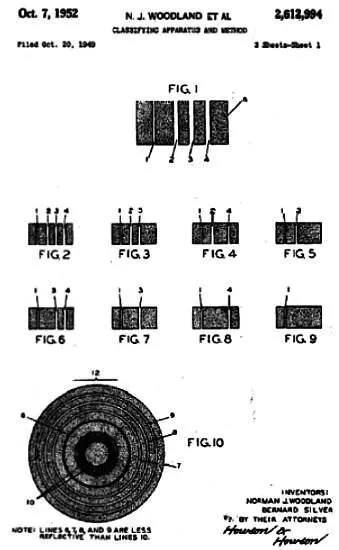
Патент системы Вудландаи Сильверас концентрическими кругами, предшественниками современных штрихкодов.

* * *

ПРОГРАММА В EXCEL ДЛЯ РАСЧЕТА КОНТРОЛЬНОЙ ЦИФРЫ КОДА EAN-13

Штрихкод стандарта EAN-13 — это номер из 12 цифр плюс тринадцатая цифра, называемая контрольной цифрой (КЦ). 13 цифр составляют четыре группы:

* * *

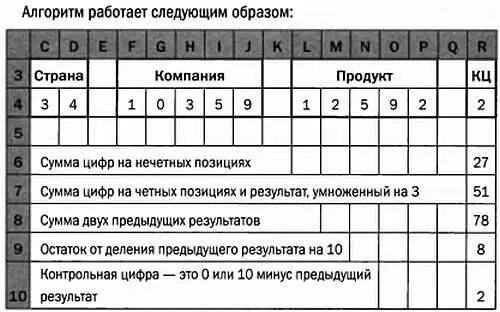
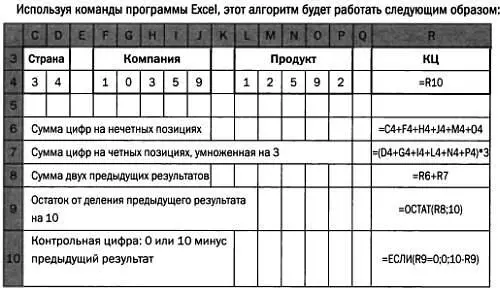
Стандарт штрихкода EAN-13

Стандарт EAN в момент создания в 1976 г. являлся аббревиатурой ( European Article Number — европейский номер товара), а сейчас известен как Международный номер товара. Это наиболее устоявшийся стандарт штрихкодов, используемый во всем мире. Штрихкоды EAN обычно состоят из 13 цифр, представленных черными полосами и пробелами, вместе образующими двоичный код, который легко читать. EAN-13 изображает эти 13 цифр с помощью 30 черных и белых полос. Цифры делятся на три группы: первая, состоящая из двух или трех цифр, обозначает код страны; вторая, состоящая из 9 или 10 цифр (в зависимости от длины кода страны), указывает компанию и продукт, и третья, состоящая из единственной цифры, выступает в качестве контрольного кода. Для штрихкода ABCDEFGHIJKLM эти группы выглядят так:

Первые три цифры (АВС) обозначают код страны, производящей товар. Для России этот код может быть от 460 до 469. Для некоторых стран этот код может быть двузначным; тогда третья цифра входит в следующую группу.

Следующие шесть цифр (DEFGHI) обозначают компанию, производящую продукт. В этой группе может быть 4–6 цифр.

Остальные три цифры (JKL) означают код продукта, который был выбран компанией. В этой группе может быть 3–5 цифр.