Жуан Гомес - Мир математики. т.4. Когда прямые искривляются. Неевклидовы геометрии

* * *

ДРУГАЯ ГЕОМЕТРИЯ, ДРУГОЙ МИР

Раструб трубы представляет собой хорошую модель гиперболической поверхности. Можно ли на этой поверхности двигаться по прямой линии? Представьте себе, что два неевклидовых жителя трубы идут по направлению к раструбу. Внешний наблюдатель увидит, что их пути постепенно расходятся. Однако, жители гиперболического мира будут продолжать двигаться по строго параллельным линиям. Хотя для ученых эта воображаемая ситуация может показаться легкомысленной, реалии гиперболического мира оказываются увлекательной идеей для научной фантастики. О гиперболических мирах было написано множество романов, включая «Опрокинутый мир» Кристофера Приста.

* * *

Такая гиперболическая модель была предложена Альбертом Эйнштейном при определении пространства-времени. Вселенная Эйнштейна четырехмерная, так как она содержит три пространственных координаты и четвертую координату — время (позже мы расскажем об этом подробнее). Человек не может воспринимать четырехмерную вселенную, поэтому трудно перенести модель с предметами на кровати (это лишь трехмерные объекты) в четырехмерное пространство. Однако мы можем представить, что произойдет. Как и в других областях математики, людям приходится полагаться на воображение и ум.

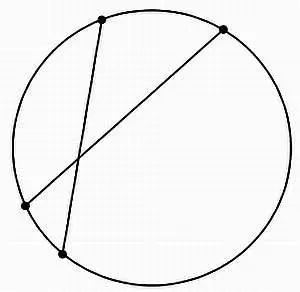
В 1870 г. немецкий математик Феликс Клейн(1849–1925) представил еще одну модель гиперболической геометрии на плоскости, а затем обобщил ее для пространства. В своей модели Клейн рассмотрел обычный евклидов круг и предложил новые определения точки, прямой, параллельной линии и так далее. Он назвал внутренность круга плоскостью, точки определил как обычные точки внутри круга, за исключением лежащих на окружности, и прямыми линиями назвал хорды круга, но не включающие концов, то есть без точек на окружности. (Напомним, что хордой круга называется отрезок, концы которого лежат на окружности.) Кроме того, параллельными прямыми он называл хорды с одним общим концом. Пересекающимися линиями назывались те, что пересекаются внутри круга, а если линии пересекаются вне круга, то они назывались непересекающимися.

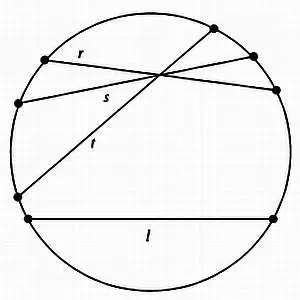
В этой модели, то есть когда плоскостью является только внутренность круга, а хорды являются прямыми линиями, мы видим, что прямые r, s и l проходят через точку вне прямой l и не пересекаются с прямой l в неевклидовом смысле, так как они не пересекаются с прямой l внутри круга. Таким образом, в этой модели через точку вне прямой можно провести бесконечное число линий, не пересекающихся с данной прямой.

Клейн показал, что геометрия в его круге эквивалентна гиперболической геометрии, то есть его геометрия удовлетворяет всем аксиомам Евклида, кроме пятого постулата, и сохраняет все результаты гиперболической геометрии.

* * *

ПРЕДЕЛ — КРУГ IV

Этот рисунок Маурица Корнелиса Эшера(1898–1972) имеет альтернативное название «Ад и рай». На нем ангелы и демоны изображены в виде мозаики, так что пространство между фигурами одного вида образует фигуры другого вида. Еще один замечательный факт: фигуры становятся все меньше и меньше по мере приближения к краю круга, как будто уходят в бесконечность. Эшер создал этот рисунок, чтобы изобразить поверхность, невозможную в двух измерениях. Свойства этого пространства знакомят нас с неевклидовой гиперболической геометрией.

* * *

Вскоре после того как Лобачевский и Бойяи построили новую геометрию, появилась другая неевклидова геометрия. Ее создал известный немецкий математик Бернхард Риман, который заменил пятый постулат Евклида другой аксиомой:

«Через точку Р , не лежащую на данной прямой l , не проходит ни одной прямой, параллельной данной».

Бернхард Риман(1826–1866) родился в Ганновере и уже в юном возрасте был математически одаренным ребенком. В 16 лет, учась в Люнебургской гимназии, он проявил большие математические способности, и директор школы разрешал мальчику брать из своей личной библиотеки книги по математике. В 1846 г. Риман поступил в Гёттингенский университет, где изучал теологию по совету своего отца. Однако, в конце концов он перешел на философский факультет, где также преподавалась математика. Его учителями были такие светила, как Мориц Штерн и сам Гаусс.

В 1847 г. Риман перешел в Берлинский университет, где преподавали Штайнер, Якоби, Дирихле и Эйзенштейн. Затем он вернулся в Гёттинген и получил докторскую степень по философии под руководством Гаусса. В 1854 г. Риман начал преподавать в университете и прочитал лекции по основам новой геометрии, но эти лекции были опубликованы лишь через два года после его смерти. Риман был избран членом Берлинской академии наук, но в конце концов был вынужден уехать из Германии для лечения от туберкулеза.

Он закончил свои дни в Италии.

Однажды, когда Риман учился у Гаусса в Гёттингенском университете, профессору нужно было выбрать одного студента в качестве представителя группы. Он придумал следующий метод отбора: «Каждый из вас предложит три темы. Руководство факультета выберет одну из них, и этот студент выступит с трехчасовым докладом по этой теме». Риман решил прокомментировать книгу Лобачевского «Новые начала геометрии». В своем предложении он написал знаменитые слова:

« Евклид утверждал, что через точку вне данной прямой можно провести только одну параллельную ей линию, Лобачевский писал, что параллельных ей линий можно провести сколько угодно, а я говорю, что нельзя провести ни одной ».

Бернхард Риман

* * *

СФЕРИЧЕСКИЙ МИР РИМАНА

С обычным воздушным шариком можно провести интересный эксперимент, который поможет лучше понять геометрию Римана. На плоском ненадутом воздушном шарике нарисуйте отрезок прямой линии и измерьте его длину. Рядом с ним нарисуйте треугольник. Если теперь шарик надуть, то рисунки на его поверхности трансформируются. Как выглядят теперь отрезок и треугольник? Остался ли отрезок прямым? Равна ли сумма углов в треугольнике 180°?

На надутом воздушном шарике прямая превращается в кривую, называемую геодезической линией, которая является большим кругом на сфере. Риман не мог провести этот простой, но наглядный эксперимент. В его время воздушные шарики еще не были изобретены.