Микель Альберти - Мир математики. т.20. Творчество в математике. По каким правилам ведутся игры разума

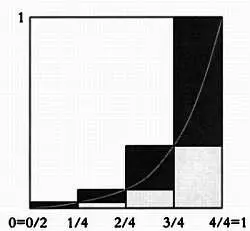
Искомая площадь S заключена между суммой площадей меньших прямоугольников S 1 (выделены светло-серым) и больших прямоугольников S s (выделены темно-серым). Точнее говоря, искомая площадь будет больше первого значения и меньше второго. Вычислим обе эти площади с учетом того, что основания всех прямоугольников одинаковы и равны 1/4, отличаются лишь их высоты:

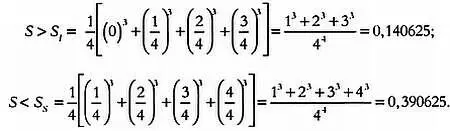
Среднее значение этих площадей равно: S ~ = ( S 1 + S s )/2 = 0,265625. Найдем более точное значение площади, разбив исходный интервал на большее число частей:

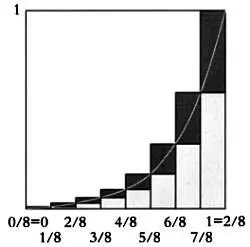
Теперь основания всех прямоугольников равны 1/8. И вновь сумма площадей прямоугольников, выделенных темно-серым ( S s ), будет больше искомой площади, которая превышает сумму площадей прямоугольников, выделенных светло-серым ( S 1 ).

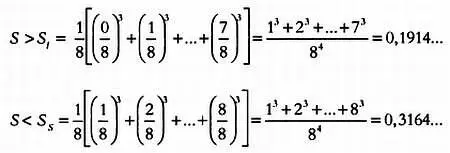
Их среднее значение равно:

S ~= 0.5·( S s + S 1 ) = 0,2539…

Если мы продолжим этот процесс и будем последовательно делить интервал [0,1] на все более мелкие части, то в пределе мы разделим его на бесконечное число частей, получим бесконечное число прямоугольников, а сумма их площадей будет равна площади фигуры, заключенной между графиком кривой и осями координат.

Вопрос в том, как вычислить общую площадь бесконечного числа прямоугольников. Произведенные выше расчеты показывают, что искомое значение должно быть близко к 0,25, так как промежуточные результаты равны 0,2656… и 0,2539…

Чтобы получить окончательный ответ, рассмотрим, как мы вычислили два предыдущих значения. Вне зависимости от числа прямоугольников, будь их восемь, сто, тысяча или n , сумма их площадей будет рассчитываться одинаково. Значение площади S s при разделении интервала [0, 1] на n равных частей будет равно:

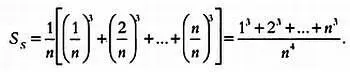
Следовательно, задача сводится к тому, чтобы найти значение этого выражения, когда n стремится к бесконечности. Посмотрим, чему равен его числитель, представляющий собой сумму кубов натуральных чисел:

1 3= 1

1 3+ 2 3= 9

1 3+ 2 3+ 3 3= 36

1 3+ 2 3+ 3 3+ 4 3= 100

Числитель будет равен 1, 9, 36, 100, … — это квадраты чисел 1, 3, 6, 10, … Может показаться, что суммы кубов натуральных чисел равны квадратам некоторых других чисел. Но каких? Какой ряд образуют числа 1, 3, 6, 10, …? Заметим, что

1 = 1

1 + 2 = 3

1 + 2 + 3 = 6

1 + 2 + 3 + 4 = 10.

Можно сформулировать теорему:

Сумма кубов первых n натуральных чисел равна квадрату их суммы.

Правильность этой теоремы можно подтвердить экспериментально для множества чисел — компьютер справится с этим за несколько мгновений. Однако экспериментальное подтверждение частных результатов и выведение из них какого-то общего принципа (именно так действуют физики и биологи) для математиков неприемлемо. В математике истинность увиденного нужно подтвердить для всех возможных случаев.

Как подтвердить истинность нашей теоремы для всех возможных случаев? Начнем с того, что вычислим сумму первых n натуральных чисел. Для этого применим метод, который использовал великий немецкий математик Карл Фридрих Гаусс, когда ему не было и десяти лет. Его биографы отмечают, что как-то раз преподаватель, чтобы занять учеников, дал им задание вычислить сумму натуральных чисел от 1 до 100.

Среди учеников был и Гаусс, который, к удивлению учителя, через несколько секунд протянул ему грифельную доску с правильным ответом. Юный Гаусс записал числа в два ряда, один над другим, и вычислил суммы в каждом столбце:

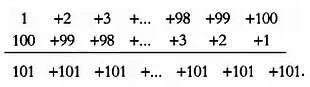
Сумма чисел в нижнем ряду равна 100·101 = 10100, что в два раза больше требуемой суммы. Следовательно, правильный ответ равен

1 + 2 + 3 + … + 99 + 100 = 10100/2 = 5050.

Применим этот же метод в нашем, более общем случае:

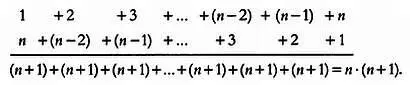
Можно заметить, что формула суммы первых n натуральных чисел такова:

1 + 2 + 3 +… + n = n ( n + 1)/2 (*)

Вернемся к нашей теореме и используем эту формулу (**):

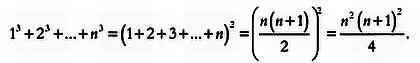
Теперь у нас есть две формулы, в которых фигурирует n первых натуральных чисел. Подтвердить правильность этих формул экспериментально на бесконечном множестве чисел невозможно. Нужно найти стратегию, которая позволила бы обойти эту проблему. Математик рассуждает так: «Отлично, дана формула, верная для n -го натурального числа. Так как все натуральные числа получаются прибавлением единицы к предыдущему, то если формула верна для n -го числа, я докажу ее истинность для следующего натурального числа. Если я докажу, что формула, верная для n, верна и для n + 1, то я автоматически докажу ее истинность для всех натуральных чисел».

Именно так мы и поступим. Сначала мы докажем, что если формула (*) верна для n , то она будет верна и для n + 1. Затем проведем аналогичное доказательство для формулы (**). Докажем, что:

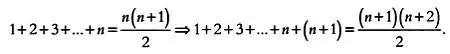
Нам всего лишь нужно показать, что разность между двумя выражениями в левой части равенства, равная n + 1, равна разности двух выражений в правой части равенства:

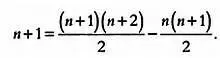
Достаточно найти значение правой части равенства, чтобы убедиться, что это в самом деле так. Аналогично доказывается истинность выражения (**). Теперь мы можем закончить решение нашей задачи о площади:

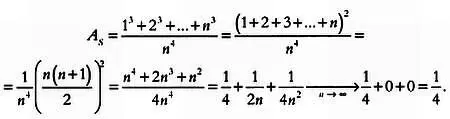
Последнее преобразование верно потому, что с ростом n значения выражений 1/2 n и 1/4 n 2становятся все меньше и меньше. В пределе, когда значение n равно бесконечности, значение обоих выражений будет равно 0. Как следствие, площадь фигуры, ограниченной кривой у = х 3, равна 1/4 = 0,25.

Наиболее выдающийся результат математического творчества, который мы применили в этом решении, таков: мы вписали в искомую фигуру, площадь которой мы хотим найти, ряд прямоугольников, площадь которых легко вычислить. Чем больше прямоугольников мы впишем в искомую фигуру, тем ближе сумма их площадей будет к площади искомой фигуры. Так как значения площадей прямоугольников в пределе приближаются к конкретному числу и мы можем это доказать, можно найти конкретное значение площади криволинейной фигуры. От геометрического параллелизма мы переходим к числовому и обратно. Мы решили более простую задачу, чем исходная, а затем использовали полученный результат для решения нужной задачи.