Бизенц Торра - Том 15. От абака к цифровой революции. Алгоритмы и вычисления

* * *

Сомножитель 1/16 n позволяет находить с помощью этого выражения знаки двоичной записи π . Еще одна из предложенных ими формул выглядит так:

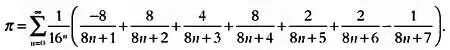
Расчеты знаков Я велись на протяжении нескольких тысяч лет, и в них участвовали наиболее выдающиеся умы в истории человечества. В настоящее время благодаря компьютерам число известных знаков π превышает несколько триллионов, однако для большинства вычислений достаточно всего нескольких знаков.

В статье, опубликованной в специализированном журнале в 1984 году, братья Борвейн констатировали удивительный факт, не углубляясь в анализ его причин:

«На практике всего 39 знаков Я достаточно для вычисления длины окружности радиуса 2·10 25метров (это расстояние больше, чем путь, который пройдет частица, движущаяся со скоростью света, в течение 20 000 миллионов лет, то есть это расстояние превышает радиус Вселенной), причем ошибка не будет превышать 10 -12метра (это расстояние меньше радиуса атома водорода). Нет никаких сомнений, что вычисление значения π с максимально возможной точностью имеет больше математическую, чем практическую ценность».

Развитие аппаратного обеспечения шло параллельно с эволюцией языков программирования. На бытовом уровне язык программирования можно определить как коммуникативный код, с помощью которого можно объяснить компьютеру, что нужно делать, чтобы решить данную задачу. Иными словами, это перечень инструкций, записанный понятным компьютеру способом в заданном порядке. Инструкции описывают последовательность действий, необходимых для получения желаемого результата. При взгляде на это определение в памяти мгновенно всплывают наши старые знакомые, о которых мы рассказали в первых главах этой книги, — алгоритмы.

И действительно, согласно более формальному определению, язык программирования — это способ описать алгоритмы, управляющие поведением компьютера.

Разумеется, инструкции языка программирования должны быть четкими и однозначными и всегда должны служить решению конкретной задачи. В языке программирования также должен быть реализован основной элемент алгоритмов и языков программирования — повтор. В языках программирования повторы реализованы двумя способами — с помощью итерации и рекурсии. Итерация — это организация обработки данных, при которой действия повторяются многократно. Она реализуется с помощью инструкций, подобных операторам repeat, while и for . Рекурсия — это повторение действий самоподобным образом, при котором процедуры вызывают сами себя.

В прошлых главах этой книги вы могли убедиться, что понятие «алгоритм» появилось намного раньше, чем компьютеры. Изначально этот термин относился к чистой математике и означал исключительно описание последовательности инструкций, необходимых для выполнения арифметических расчетов. Лишь позднее это понятие стали использовать в более широком смысле и связывать с информатикой, столь популярной в наши дни. Языки программирования — это всего лишь следующий этап эволюции форм записи алгоритмов, более формальный и точный (в противном случае они не могли бы быть использованы в компьютерах).

* * *

ТЕРМИН «РЕАЛИЗАЦИЯ»

Реализация — это осуществление или воплощение чего-либо. В информатике этот термин означает запись определенного алгоритма на заданном языке программирования.

ТЕРМИН «ПРОГРАММИРОВАНИЕ»

Слово «программировать» (англ, to program ), означающее задание инструкций, которые должен выполнить компьютер, было придумано группой исследователей, работавших над созданием компьютера ENIAC в Институте Мура Пенсильванского университета. В то время использовалось слово «настраивать» ( to set up ), так как программирование ENIAC (изображен на иллюстрации ниже) осуществлялось с помощью соединений и переключателей, то есть путем изменения электрической схемы самого компьютера. Постепенно, по мере того как разделение между аппаратным и программным обеспечением становилось все более явным, стало применяться слово «программирование».

* * *

Древнейшие алгоритмы, которые позволили вавилонянам провозгласить себя первыми математиками, способными решать достаточно сложные задачи, использовались для решения алгебраических уравнений, записывались в общем виде и демонстрировались на конкретных примерах. В них не использовались итерации или условные конструкции вида « если x< 0, то », так как вавилонянам не был известен нуль. Чтобы выразить несколько возможных вариантов, математики Вавилонии повторяли алгоритм необходимое число раз. Прошло много веков, прежде чем Евклид примерно в 300 году до н. э. описал алгоритм вычисления наибольшего общего делителя двух чисел. Этот алгоритм, который сегодня известен как алгоритм Евклида, как правило, реализуется с помощью рекурсии.

* * *

РЕАЛИЗАЦИЯ АЛГОРИТМА ЕВКЛИДА

Приведем в качестве примера реализацию алгоритма для нахождения наибольшего общего делителя чисел Аи Всначала на языке Пролог, затем на языке Java. Сокращение gcdозначает great common divisor — наибольший общий делитель.

В реализации на языке Пролог использованы три правила, соответствующие трем возможным случаям. Во всех случаях два первых аргумента являются числами, третий аргумент можно интерпретировать как результат. В первом правиле второй аргумент принят равным нулю. Второе правило применяется тогда, когда первый аргумент больше второго, третье правило — когда второй аргумент больше первого.

gcd (А, 0, А).

gcd (А, В, D)(А > В), (В > 0), R is A mod В, gcd(B, R, D).

gcd (А, В, D)(А < В), (А > 0), R is В mod A, gcd(A, R, D).

В реализации на языке Java также используются вышеизложенные правила. В качестве входных параметров использованы два числа Аи В, в качестве результата функция возвращает их наибольший общий делитель. Первая версия алгоритма является рекурсивной, вторая — итеративной.

public static int gcd (int A, int B) {

if (B == 0) {return A;}

else if (A > B) {return gcd(B, A % B);}

else if (A < B) {return gcd(A, В % A);}

return 1;

}

public static int gcdlterative (int A, int B) {

int r = 0;

while (B > 0) {