Бизенц Торра - Том 15. От абака к цифровой революции. Алгоритмы и вычисления

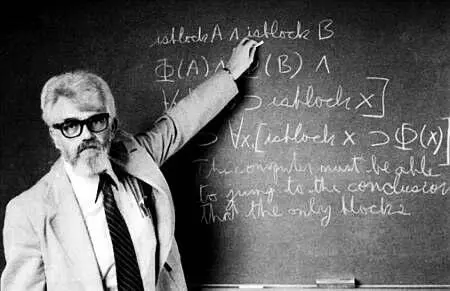
Джон Маккарти, создатель термина «искусственный интеллект». Стэндфордский университет, 1980 год.

* * *

ЛЯМБДА-ИСЧИСЛЕНИЕ

Эта система была разработана Алонзо Чёрчем и Стивеном Клини в начале 1930-х годов. Ее возможности были эквивалентны возможностям машины Тьюринга, но основной принцип лямбда-исчисления был иным. С формальной точки зрения в лямбда-исчислении используются выражения и правила преобразования выражений, которые моделируют использование функций и вычислений. Рассмотрим в качестве примера определение истинности и ложности:

истина: λху. х

ложь: λху. у.

Логическая функция «И» определяется так:

И: λpq.p q р.

Чтобы найти значение выражения «истина ложь», заменим каждый член этого выражения его эквивалентом с точки зрения лямбда-исчисления:

(λpq.p q р) (λху. х) (λху. у).

Применив правила записи, получим выражение (λху. у), что, как мы уже говорили, эквивалентно значению «ложь». Числа и операции с числами определяются аналогично.

* * *

В языке LISP данные и программы представляются одинаковым образом. Основной парадигмой этого языка является рекурсия, что позволяет избежать нежелательных побочных эффектов императивного программирования. В этом языке также были введены условные выражения и префиксная (польская) нотация Яна Лукасевича.

* * *

ПРЕФИКСНАЯ (ПОЛЬСКАЯ) НОТАЦИЯ

Математические выражения в этой нотации обозначаются символом, соответствующим операции, который располагается перед операндами. Так, выражение

( а+ Ь) — ( с· d)

в польской записи будет выглядеть так:

- + ab · cd.

* * *

В середине 1960-х Питер Лэндин создал новый функциональный язык ISWIM(от англ. If You See What I Mean — «если ты видишь, что я имею в виду»), в основе которого находился язык LISP и лямбда-исчисление. На основе языка ISWIM было разработано целое семейство функциональных языков ( ML, FP, Mirandaи другие).

В то время функциональное программирование было интересно лишь немногим исследователям. Оно начало набирать популярность в 1978 году, когда Джон Бэкус, создатель языка Фортран, опубликовал статью «Можно ли освободить программирование от стиля фон Неймана?» Бэкус критиковал традиционные языки программирования и выступал за развитие новой парадигмы, которую он назвал «функциональное программирование». В ней делался акцент на функционалы (функции, аргументами которых являются другие функции). В своей статье, за которую он был удостоен премии Тьюринга, Бэкус описал язык FP( Functional Programming ), в котором не использовались переменные. Статья пробудила интерес исследователей к функциональным языкам и привела к появлению новых подобных языков.

В настоящее время существует два обширных семейства функциональных языков. Первое образовано языками, созданными на основе LISP, второе — языками, созданными на основе ISWIM. К первому семейству принадлежат разновидности языка LISP, например Common LISP, и самостоятельные языки, например Scheme.

Ко второму семейству принадлежит язык Standard ML— результат стандартизации языков MLи Норе, созданных в Эдинбургском университете. ML в отличие от LISP является строго типизированным функциональным языком ( strongly-typed language ). Это означает, что все выражения в этом языке имеют тип, который определяется системой во время компиляции (статический тип). Кроме этого, программист может вводить новые типы, определяя абстрактные типы данных. Язык ML допускает определение модулей и общих модулей, которые называются функторами. В языке Норе, в отличие от ML, типы требуется определять явно.

* * *

ФУНКЦИОНАЛЬНЫЕ ЯЗЫКИ: ПРИМЕРЫ РЕАЛИЗАЦИИ

Ниже приведены примеры определения функции факториала на разных языках программирования. Обратите внимание на схожесть синтаксиса языков, принадлежащих к двум основным семействам функциональных языков. В языках, подобных USP( Scheme, Норе и ML ), используются переменные, определение факториала является рекурсивным и напоминает его определение на языке Java, которое приводилось несколькими страницами ранее. В языке FP, напротив, переменные не используются. В определении на языке FP используется функция iota. Эта функция возвращает список всех натуральных чисел, меньших заданного числа. К этому списку применяется конструкция / *, осуществляющая умножение его элементов. Конструкция /opрасширяет бинарную операцию, применяя ее ко всем элементам списка.

Определение на языке LISP :

(defun factorial (n) (if (= n 0) 1 (* n (factorial (- n 1)))))

Определение на языке Scheme :

(define factorial

(lambda (n)

(if (= n0) 1 (*n (factorial (-n 1))))))

Определение на языке Hope :

dec fact: num — > num;

- - - fact 0 < = 1;

- - - fact n < = n*fact(n — 1);

Определение на языке ML

fun f (0: int): int = 1

|f (n: int): int = n * f(n — 1)

Определение на языке FP :

fact =/* op iota

* * *

БЕСКОНЕЧНЫЕ СПИСКИ ЯЗЫКА HASKELL

Следующие определения двух бесконечных списков на языке Haskellпомогут вам понять разницу между «жадными» и «ленивыми» вычислениями. Эти определения являются рекурсивными, то есть используют сами себя.

Первое определение соответствует списку натуральных чисел. По индукции предполагается, что список уже определен корректно. Все элементы списка увеличиваются на единицу, таким образом, получается список 2, 3, 4…., к которому добавляется единица. В определении все элементы списка натуральных чисел увеличиваются на единицу с помощью конструкции « mар (+1) naturales ».

Второе определение соответствует списку чисел Фибоначчи. Предположим, что этот список уже определен. В определении списка чисел Фибоначчи каждому числу ставится в соответствие следующее число, затем вычисляется сумма в каждой такой паре чисел. В определении « listafibs » ставится в соответствие «хвосту» listafibs , который получается с помощью конструкции « tail listafibs ». Далее соответствующие элементы двух списков складываются с помощью конструкции « zipWith (+) ».

naturales= 1: map (+1) naturales

listafibs= 0:1: zipWith (+) listafibs (tail listafibs)

Эти определения являются корректными, так как в них используются «ленивые» вычисления. Если бы в них, как в большинстве других языков, использовались «жадные» вычисления, то компьютер обрабатывал бы эти определения бесконечно долго. Обратите внимание, что для определения натуральных чисел сначала требуется выявить бесконечный список, после чего прибавить единицу ко всем его элементам.