Энрике Грасиан - Том 18. Открытие без границ. Бесконечность в математике

Множество, образованное всеми подмножествами А , называется множеством-степенью A и обозначается 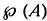. Кантор доказал, что для любого множества его множество-степень больше, чем само множество, то есть оно содержит больше элементов, или, если быть математически корректными, его кардинальное число больше, чем у исходного множества. Будем обозначать кардинальное число А как | А |.

Изложенный выше результат можно записать так:

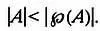
Ученому принадлежит доказательство нескольких теорем, но когда речь идет о теореме Кантора, обычно имеют в виду именно этот результат, который можно записать в виде

| А | < 2 | A |

Теорема Кантора позволяет упорядочивать бесконечности. Кантор считал, что «самая маленькая» бесконечность соответствует кардинальному числу множества — множества натуральных чисел. Это кардинальное число он обозначил .

Таким образом, имеем

| | =

По теореме Кантора получим:

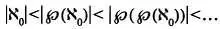
Последовательность кардинальных чисел, фигурирующую в этом неравенстве, Кантор назвал числами алеф, присвоив каждому из них порядковый номер: алеф-ноль, алеф-один и т. д. Они записываются буквой еврейского алфавита алеф с индексом:

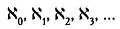
Это так называемые трансфинитные числа.

В упорядоченной последовательности трансфинитных чисел содержится любое число, которое может существовать, в том числе такое, которое мы даже не можем себе представить. Если до Кантора считалось, что ничто не может быть больше бесконечности, то благодаря его открытиям мы можем с уверенностью утверждать, что всегда существует другая бесконечность, которая будет больше данной. Кантор превзошел самого Создателя: сколь большое число ни создал бы Бог, всегда будет существовать другое, большее число. И этот научный результат противоречил религиозным взглядам самого Кантора.

* * *

ПОЧТИ БЕСКОНЕЧНОСТЬ

За рамки нашей конечной природы выходят не только бесконечные или трансфинитные числа.

Например, число

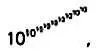
которое может быть результатом неких математических расчетов, невероятно велико. Процессор компьютера, выполнив необходимые инструкции, может получить это число за разумное количество шагов. Это возможно потому, что и язык математики, и языки программирования предоставляют все необходимые для этих вычислений инструменты. Но если бы нам потребовалось записать все цифры этого числа на бумаге, мы не смогли бы этого сделать: для такой записи требуется лист бумаги, число частиц в котором превышает число частиц во всей Вселенной. Кроме того, для записи этого числа потребовалось бы время, значительно превышающее возраст Вселенной.

* * *

Пока что мы говорили о кардинальности применительно к множеству. Мы увидели, что понятие кардинальности обозначает число элементов множества, а также что каждому элементу конечных множеств можно последовательно присвоить натуральное число. С другой стороны, когда речь идет о множествах с бесконечным числом элементов, пронумеровать их составляющие можно с помощью взаимно однозначного соответствия, при котором каждому элементу множества ставится в соответствие натуральное число. Множества, для которых возможно установить такое соответствие, называются счетными. Однако мы также увидели, что существуют множества, которые не являются счетными, и чтобы как-то обозначить количество их элементов, нам пришлось обратиться к понятию кардинальности. Таким образом, кардинальность множества — это не совсем число, а скорее понятие, связанное с числовой величиной. По сути, на этом понятии основан удивительный трюк, позволяющий узнать, насколько велико множество. Заключается он в сравнении множеств по определенным правилам, которые позволяют однозначно сказать, когда множества одинаково велики, а когда — нет. При этом не имеет значения, о конечных или бесконечных множествах идет речь.

* * *

СВОБОДА МАТЕМАТИКИ

Можно сказать, что в настоящее время мечта Кантора о свободной математике полностью сбылась. По меньшей мере, никто и ничто (в так называемых цивилизованных странах) не ставит палки в колеса авторам математических теорий по философским или религиозным причинам. Сегодня в математике используются так называемые «большие кардиналы», которые столь велики, что рядом с ними трансфинитные числа Кантора кажутся карликами. Их определение очень сложно, хотя они строятся по правилам, схожим с теми, что применяются к алеф-числам: рассматривается последовательность множеств, включенных одно в другое, затем анализируются соответствующие множества их частей.

* * *

Кантор назвал алеф-нулем кардинальное число множества натуральных чисел | | = , а кардинальное число множества вещественных чисел он обозначил термином «континуум» и символом с . Сделал он так потому, что вещественные числа полностью заполняют вещественную прямую, а так как эта прямая представляет собой непрерывную последовательность чисел (в ней отсутствуют промежутки), ее можно обозначить словом «континуум» (от лат. continuum — «непрерывное»).

В соответствии с этим

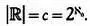
Однако числа алеф образуют возрастающую последовательность

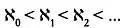
Здесь Кантор сформулировал следующий вопрос: существует ли такой кардинал, который заключен между кардинальным числом множества натуральных чисел и континуумом? Каким-то образом ему удалось понять, что выполняется равенство

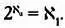
Иными словами, не существует множества, размер которого заключен между размером множества натуральных и вещественных чисел, — эта гипотеза называется континуум-гипотезой. Чтобы доказать ее, Кантору потребовалось приложить невероятные усилия. Не раз он считал, что континуум-гипотеза доказана, но ему так и не удалось сформулировать доказательство, которое его полностью устраивало бы.

Континуум-гипотезу безуспешно пытались доказать многие современники Кантора, в том числе Гильберт, Рассел и Цермело. Венгерский математик Денеш Кёниг(1849–1913) на конгрессе в Гейдельберге в 1904 году представил доказательство ложности континуум-гипотезы. Но Кантор верил своей интуиции и считал, что доказательство Кёнига не может быть истинным, хотя так и не смог найти в нем ошибку. Обнаружил ее Цермело, таким образом, вопрос доказательства континуум-гипотезы оставался открытым, и Гильберт включил его в свой знаменитый список из 23 наиболее важных нерешенных задач математики.