Франсиско Мартин Касальдеррей - Мир математики. Том 16. Обман чувств. Наука о перспективе

Утром 8 ноября испанцы перешли в наступление, и деморализованные англичане под непрекращающимся обстрелом покинули поле сражения. Этот подвиг, как и взятие Бреды, изобразил на театральной сцене драматург Родриго де Эррера в пьесе La fe no ha menester de armas у venida del inglés a Cadiz («Вере не страшно оружие и нападение англичан на Кадис»).

Привлекает внимание историческая точность картин, ставшая возможной благодаря тому, что между изображаемыми событиями и написанием картины прошло всего несколько лет. Король и граф-герцог де Оливарес, несомненно, были знакомы с героями картин, поэтому эти полотна также выступали в качестве групповых портретов. Однако композиция картин выглядит странно: передний план, на котором изображены действующие лица, и задний план, где изображен пейзаж, плохо согласуются между собой. Можно подумать, что на картине изображен эпизод театральной постановки, то есть персонажи показаны на фоне плоской декорации. Кроме того, портреты действующих лиц непропорционально вытянуты.

В настоящее время картина выставлена в музее Прадо, где занимает целую стену небольшого зала и отстоит от пола менее чем на полметра. Создается впечатление, что Сурбаран не владел законами перспективы — именно это утверждают многие критики.

Если взглянуть на картину с точки зрения математики, то станет ясно, что причина этому в неверном расположении картины в музее. Сурбаран деформировал изображение умышленно, чтобы скомпенсировать искажения, возникавшие при взгляде на картину, когда она располагалась в предназначенном для нее месте. Таким образом, при взгляде на картину зритель должен был видеть безупречное изображение.

Математический взгляд на «Оборону Кадиса»

Первая гипотеза, которую мы рассмотрели, заключалась в том, что картина должна висеть выше. Попробуем определить, насколько именно. Если мы поместим прямоугольник на возвышение и будем смотреть в его центр, то нам будет казаться, что он имеет форму равнобедренной трапеции. Величина искажения будет зависеть от высоты h , на которой расположен прямоугольник, и расстояния d между картиной и зрителем. Значение d , соответствующее размерам картины, равняется примерно 4,5 м. Осталось определить величину h , а еще лучше — зависимость длины верхней стороны трапеции и ее высоты от h . Оценить эту зависимость нетрудно, если произвести некоторые тригонометрические расчеты. Расчеты показывают, что картина, скорее всего, располагалась так, что нижний край рамы находился на уровне глаз наблюдателя. Однако, как вы увидите далее, рассуждения можно упростить, применив некоторые законы геометрии. Примем эту гипотезу в качестве исходной и попробуем доказать ее экспериментально.

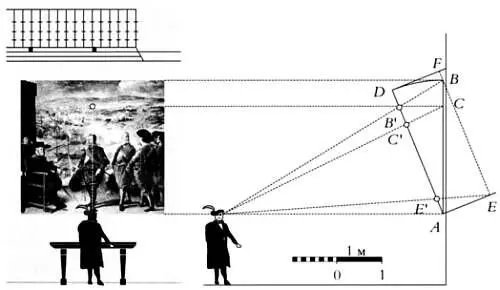
Проекция главного луча зрения наблюдателя на картину «Оборона Кадиса против англичан».

(источник: FMC)

Перенесемся в Зал королей и посмотрим на картину Сурбарана с расстояния примерно в 4,5 метра. Предположим, что картина расположена на уровне наших глаз, как показано на предыдущем рисунке. Точка схода располагается в центре линии горизонта и обозначена на рисунке. Справа приведем изображение этой сцены в профиль. Для этого перенесем на рисунок справа отрезок АВ , длина которого равна высоте картины, и точку схода С . Зритель смотрит в точку С , следовательно, изображение, которое он видит, располагается в плоскости AD . Эта плоскость перпендикулярна линии, соединяющей точку С и точку зрения. Картина будет казаться наклоненной: верхняя часть будет располагаться дальше от наблюдателя, чем нижняя, поэтому будет казаться более узкой. Кроме того, из-за наклона высота картины будет казаться меньше. Попробуем определить, как изменятся воспринимаемые размеры картины.

Зритель видит картину так, как будто бы она наклонена внутри рамки, обозначенной буквами AEFD . Спроецируем верхнюю точку картины В на эту рамку и получим точку Е . Если зритель посмотрит сначала в точку Е , а затем в точку В , то лучи зрения пересекут плоскость изображения в точках Е' и В' соответственно.

Наконец, луч зрения, направленный в точку С , пересечет плоскость изображения в точке С' . Теперь попытаемся изобразить картину так, как ее будет видеть зритель. Мы определили три точки на плоскости изображения: В', С' и Е' . Перенесем эти точки на картину, чтобы вычислить размеры трапеции, которую будет видеть зритель.

Расположим зрителя справа, перед картиной. Точки В', С' и Е' перейдут в точки В", С" и Е" соответственно. Точка В" определяет высоту, на которой для наблюдателя будет располагаться верхний край картины. Точка С" определяет положение линии горизонта. В центре линии горизонта будут сходиться линии пола, изображенные в перспективе. Наконец, проведя горизонтальную линию через точку Е' , получим две точки пересечения с линиями, сходящимися в точке схода. Перенеся эти точки вертикально вверх, получим две точки, которые будут располагаться на горизонтальной линии, проведенной через точку В" . Соединив эти две точки с линией основания картины, получим трапецию, в которую будет вписано изображение, видимое зрителем.

Если мы рассмотрим эту трапецию, обозначенную на картине белыми линиями, то нам покажется, что она будто наклонена к нам. Анаморфированное изображение картины будет вписано в трапецию.

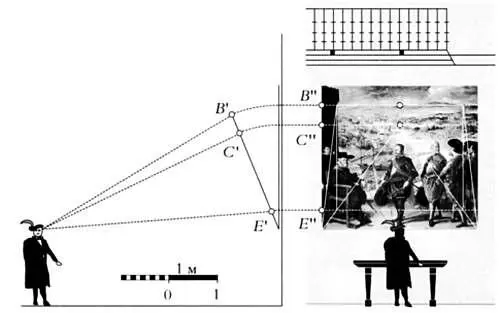
Деформированное изображение картины «Оборона Кадиса против англичан», какой ее видит наблюдатель.

(источник: FMC)

Благодаря программам обработки изображения выполнить это преобразование несложно. Получив требуемое изображение с помощью одной из этих программ, мы сможем представить, какой эта картина выглядела в глазах зрителя, проходившего по Залу королей дворца Буэн-Ретиро. Она казалась бы ему примерно такой, как показано на иллюстрации:

Анаморфированное изображение картины «Оборона Кадиса против англичан». Именно так эту картину видели зрители, когда она располагалась на изначально задуманном месте.

Персонажи изменились внешне и не кажутся короткоголовыми и полными, фон обрел глубину и реалистичность. Теперь он действительно похож на реальный пейзаж, а не театральную декорацию. Всё встало на свои места и обрело должные пропорции.