Франсиско Мартин Касальдеррей - Мир математики. Том 16. Обман чувств. Наука о перспективе

Леон Баттиста Альберти. Портрет кисти Мазаччо. Капелла Бранкаччи, Флоренция.

(источник: FMC)

* * *

Пьеро делла Франческа использовал метод Альберти в своей книге «О перспективе в живописи», упростив его. Вместо вспомогательного рисунка, как советует Альберти, он объединяет построение продольных и поперечных линий на одном рисунке, как показано ниже:

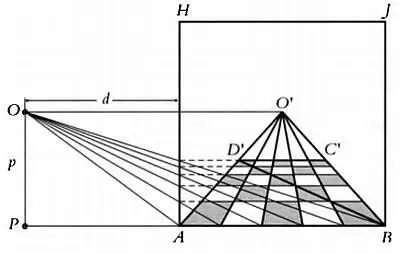
Схема перспективы по Пьеро делла Франческа.

(источник: FMC)

Этот метод, несомненно, упростил работу художника, однако по сути ничем не отличался от метода Альберти, теоретические основы которого, в свою очередь, сформулировал Брунеллески. Пьеро делла Франческа изображает в перспективе квадрат ABCD , сторона АВ которого совпадает с нижней границей картины. Он обозначает точку зрения О' , в которой сходятся стороны квадрата, перпендикулярные картинной плоскости. Далее он определяет на картинной плоскости поперечную прямую C'D' , параллельную АВ . Вид спереди и вид сбоку накладываются. Так, линия АН является не только стороной картины, но также изображением самой картины в профиль. Точка О обозначает глаз наблюдателя, который находится на расстоянии d от картинной плоскости АН . Он проводит линию из точки О в точку В , и пересечение этой линии с прямой АН определяет положение поперечной линии C'D' относительно АВ .

Кроме того, он указывает способы представления различных плоских фигур в перспективе. Для этого он вписывает эти фигуры в квадрат и использует так называемый метод точек схода. Попробуем вкратце объяснить этот метод.

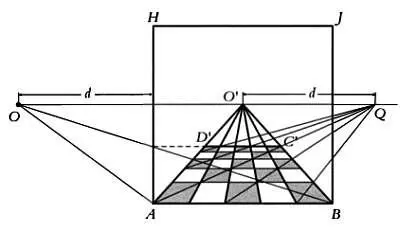
Диагонали квадратов, на которые разделен пол, сходятся в так называемой точке схода — точке Q.

(источник: FMC)

Все горизонтальные линии, параллельные между собой, вне зависимости от их положения в пространстве сходятся в перспективе в одной точке на линии горизонта. Если эти линии образуют с картинной плоскостью угол в 45°, как, например, диагонали квадратов, на которые разделен пол, изображенных на предыдущем рисунке, то точка схода этих линий будет находиться на определенном расстоянии от центра перспективы О' . Это расстояние будет равно расстоянию d от наблюдателя до картинной плоскости. Эта точка Q называется точкой схода. Очевидно, что на линии горизонта будут расположены две точки схода: одна справа от центра перспективы, другая слева.

Этот метод Пьеро делла Франческа описал в своей книге «О перспективе в живописи» так, как показано ниже:

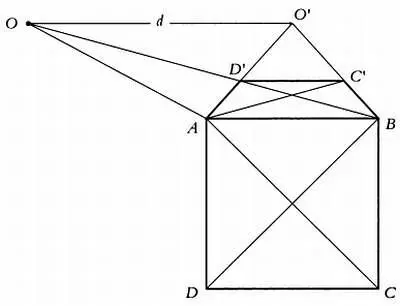
Метод точек схода, описанный Пьеро делла Франческа.

(источник: FMC)

Допустим, нужно представить в перспективе квадрат со стороной АВ , зная, на какой высоте от АВ находится точка зрения О' , и расстояние d от нее до картинной плоскости. Для этого нужно провести через точку О' , прямую, параллельную АВ , и продолжить ее до точки О , расположенной на расстоянии d от точки О' . Из точки О проведем линию в точку В , которая пересечет отрезок АО' в точке D' . И наконец, проведем через D' прямую, параллельную АВ , которая пересечет ВО' в точке С. ABC'D' будет перспективным изображением ABCD .

Пьеро делла Франческа также описал метод для определения положения любой точки квадрата в перспективе. Этот метод, который известен под названием метода диагоналей, впоследствии изложил Альбрехт Дюрер в своей книге «Руководство к измерению циркулем и линейкой». Процитируем фрагмент этой книги Дюрера:

«Когда ты хочешь представить на плоскости, видимой в перспективе, данную точку квадрата, проследуй так: начерти квадрат ABCD так, чтобы АВ была верхней горизонтальной его стороной. Нарисуй квадрат в перспективе, ABGF , лежащий на нем. Пусть О будет точкой взгляда на твой рисунок. Выбери любую точку Е квадрата. Далее проведи диагональ АС этого квадрата.

Нарисуй ту же диагональ BF в квадрате, изображенном в перспективе. Затем проведи из точки Е параллельную к стороне квадрата и продли ее до горизонтали АВ . Обозначь эту точку Н . Проведи из этой точки Н прямую линию в точку взгляда О , которая пересечет квадрат, изображенный в перспективе.

Она пересечет горизональ FG в некоторой точке. Обозначь эту точку М . Затем проведи в квадрате прямую, параллельную АВ , через точку Е до диагонали АС . Обозначь эту точку J . Проведи теперь через J параллельную стороне квадрата до АВ и обозначь эту точку К . В квадрате, изображенном в перспективе, проведи через К прямую до точки О , которая пересечет диагональ FB в точке L . И наконец, проведи из точки L горизонталь, параллельную АВ , до линии НМ . Обозначь эту точку N . Это и будет искомая точка в квадрате, изображенном в перспективе, что можно видеть на рисунке, который я изобразил ниже».

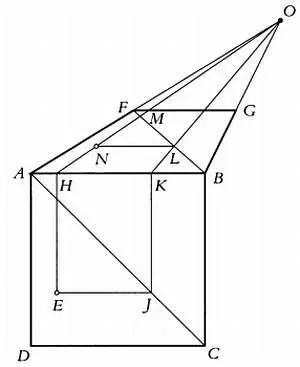
Метод диагонали, описанный Дюрером, для изображения точки в перспективе.

(источник: FMC)

В двух изданиях «Руководства к измерению циркулем и линейкой» Дюрер описал механические устройства, упрощающие рисование в перспективе. В первом издании от 1525 года упоминаются два приспособления. Они изображены на гравюрах «Портретист» и «Художник, рисующий лютню». В издании от 1538 года, отпечатанном после смерти художника, упоминаются еще два устройства, изображенные на гравюрах «Художник, рисующий кувшин» и «Техника рисования в ракурсе». Некоторые из них уже были известны таким художникам, как Донато Браманте или Альберти. Устройство, изображенное на гравюре «Художник, рисующий лютню», возможно, было изобретено самим Дюрером, который привел инструкции по его постройке.

На гравюре «Художник, рисующий лютню» изображено одно из устройств Дюрерадля рисования в перспективе.