Иоланда Гевара - Том 38. Измерение мира. Календари, меры длины и математика

Теория гомоцентрических сфер стала объектом критики уже в древности: расстояние между любой данной планетой и Землей считалось неизменным, и было непросто объяснить, почему планеты во время попятного движения светят ярче (изменение яркости планет связывалось с их приближением к Земле).

Аристотель заложил основы античной физики, объяснив движение небесных тел и проведя четкое различие между небесной динамикой (движением в надлунном мире) и земной динамикой (движением в подлунном мире). Его физическая доктрина стала догмой для 60 последующих поколений, поскольку она была крайне подробной и не противоречила здравому смыслу и наблюдениям.

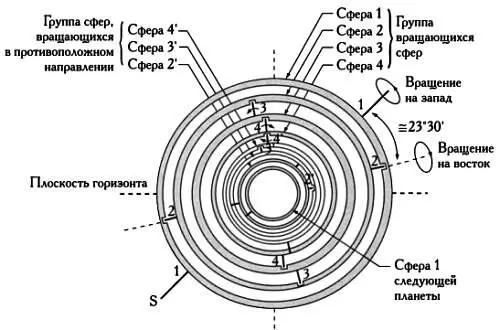
Модель Аристотеля. Первые четыре сферы соответствуют Сатурну. За исключением сферы 1, которая сообщает остальным движение на запад, движение трех других сфер (2, 3, 4) для следующих планет компенсируется движением трех сфер, вращающихся в обратном направлении (4', 3' и 2').

Аристотель не ограничился тем, что принял на веру геоцентрическую и геостатическую модель, в которой планеты двигались по круговым орбитам, — он весьма умело и остроумно доказал ее истинность. В своей космологии он установил тесную взаимосвязь между астрономией и физикой и создал настоящую систему мира — космофизику. Поэтому неудивительно, что все греческие, арабские и христианские астрономы, за редкими исключениями (одним из них стал Аристарх Самосский), явно или неявно разделяли основные предпосылки космологии Аристотеля: замкнутый и конечный космос, неподвижность Земли, расположенной в центре мира, и наличие двух принципиально разных миров — надлунного (небесного) и подлунного (земного).

О жизни Аристарха Самосского(ок. 310 г. до н. э. — ок. 230 г. до н. э.) , который был учеником Стратона из Лампсака, третьего главы Ликея, известно немногое. Все сведения о нем взяты из его книги «О величинах и расстояниях Солнца и Луны» и упоминаний более поздних авторов. Его считали авторитетным астрономом, называли математиком и отмечали его обширные знания в геометрии, астрономии, музыке и других науках. Его современник Архимед(ок. 287 г. до н. э. — ок. 212 г. до н. э.) в своем труде «Исчисление песчинок» утверждает: Аристарх предполагал, что Солнце и сфера, на которой закреплены звезды, неподвижны, а Земля вращается вокруг Солнца по кругу.

Книга «О величинах и расстояниях Солнца и Луны» — это астрономический трактат, в котором с помощью геометрических методов рассчитаны соотношения расстояний между небесными телами. В современном языке эти соотношения обозначаются синусами углов. Свои геометрические методы Аристарх позаимствовал из теории пропорций Евдокса, изложенной в книге V «Начал» Евклида. Он применил и другие соотношения, которые мы относим к тригонометрии, считая их известными или тривиальными. Он сравнил расстояние Земля — Солнце с расстоянием Земля — Луна и вычислил, что первое почти в 20 раз больше второго (истинное соотношение между этими расстояниями намного больше — 390:1).

Почему последователи Аристарха не приняли его гелиоцентрическую модель и ее вновь предложил лишь Николай Коперник в своем труде «О вращении небесных сфер» (1343)? Чтобы ответить на этот вопрос, нужно перенестись из XXI века в III век до н. э. Утверждать, что Земля движется, значило попрать древнее учение, здравый смысл и физику Аристотеля. Кроме того, если бы Земля двигалась, то наблюдался бы параллакс звезд, чего отмечено не было. Помимо этого, другие возможные преимущества этой модели (так, с ее помощью можно было объяснить изменение блеска планет) вскоре были сведены на нет при помощи новых методов, не противоречивших традиционной космологии.

* * *

ОТНОШЕНИЕ РАССТОЯНИЙ «ЗЕМЛЯ — ЛУНА» И «ЗЕМЛЯ — СОЛНЦЕ» ВЫЧИСЛЕННОЕ АРИСТАРХОМ САМОССКИМ

В III веке до н. э. Аристарх Самосский вычислил, насколько дальше Земля располагается от Солнца, чем от Луны, а также определил их относительные размеры. Для этого он использовал следующее соотношение: треугольник ЗЛС, в вершинах которого находятся Земля, Солнце и молодая Луна, прямоугольный, так как угол Земля — Луна — Солнце равен 90°. Далее он измерил угол между Солнцем и Луной и принял его равным 87°. Так как сумма углов треугольника равна 180°, β = 3°.

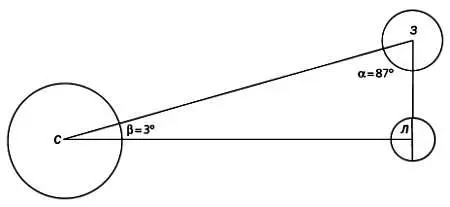
Таким образом он смог вычислить отношение расстояний d(3, С)/ d(3, Л) путем математических рассуждений. В упрощенном виде и в современной нотации суть рассуждений Аристарха записывается так:

cos 87° = d(T,L)/d(T,S),

где d(3, С) — расстояние от Земли до Солнца, d(3, Л) — расстояние от Земли до Луны:

d(T,S) = d(T,L)/cos 87°

так как 1/cos87°равняется примерно 19, имеем:

d(T,S) ~= 19d(T,L).

Кроме того, так как Луна и Солнце наблюдаются с Земли под одним и тем же углом, равным половине градуса, отношение их диаметров будет таким же:

диаметр Солнца = 19 диаметров Луны.

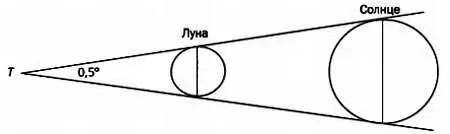
Этот математический метод остроумен и точен, однако Аристарх допустил ошибку при измерении угла α: он равен не 87°, а 89°52’ (Солнце расположено примерно в 390 раз дальше от Земли, чем Луна).

* * *

Гиппарх Никейский(ок. 190 г. до н. э. — ок. 120 г. до н. э.) применил новые измерительные приборы и первым количественно оценил неравномерности в движении Солнца и Луны. Он стал образцом для подражания для всех астрономов Александрии: пытаясь увязать принцип кругового движения с результатами наблюдений, он отдавал безоговорочный приоритет последним. Программа астрономических исследований Гиппарха выглядела так: астроном должен определить число круговых орбит небесных тел, их размеры и положение, а также скорость кругового движения, чтобы с помощью геометрических методов и численных расчетов показать, что предложенная система объясняет результаты наблюдений, позволяет делать точные количественные прогнозы и составлять прогнозные таблицы.

Гиппарх отметился важными результатами наблюдений, составил более точную карту звездного неба, систематизировал множество результатов, полученных вавилонскими астрономами, а также открыл предварение равноденствий (постепенное смещение точек равноденствия, или точек пересечения небесного экватора с эклиптикой, в силу которого равноденствия наблюдались раньше).