Иоланда Гевара - Том 38. Измерение мира. Календари, меры длины и математика
- Название:Том 38. Измерение мира. Календари, меры длины и математика
- Автор:
- Жанр:
- Издательство:«Де Агостини»
- Год:2014
- ISBN:978-5-9774-0732-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Иоланда Гевара - Том 38. Измерение мира. Календари, меры длины и математика краткое содержание
Измерения играют важнейшую роль в современной науке, но без них немыслима и повседневная жизнь. Например, без измерений невозможно узнать, что находится рядом с нами, а что — вдали. Если мы составим список всех измерений, которые проводим в течение дня, то удивимся тому, каким длинным он будет. За свою историю человечество выработало различные методы измерений. С их помощью мы смогли определить размеры нашей планеты, протяженность межзвездного пространства и даже измерить время. В этой книге пойдет речь о математических методах, на которых строятся астрономические, геодезические, календарные и метрологические измерения.
Том 38. Измерение мира. Календари, меры длины и математика - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
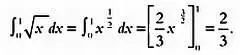
Возведение в куб
Кубом называется не только правильный многогранник, каждая сторона которого представляет собой квадрат, но и результат умножения числа на само себя трижды, то есть возведения в третью степень. Это совпадение не случайно — если мы возведем число в третью степень, то есть умножим его на само себя трижды, то получим объем куба, сторона которого выражается этим числом.
Если с квадратурой была связана классическая древнегреческая задача о квадратуре круга, то с возведением в куб — задача об удвоении куба. По легенде, эпидемия чумы, разразившаяся в Афинах в 428 году до н. э., так напугала горожан, что афинским правителям пришлось обратиться за помощью к богу Аполлону. Дельфийский оракул при храме Аполлона сказал, что если построить жертвенник в два раза большего объема, чем тот, что находился в храме Аполлона, то чума прекратится. Хотя со временем эпидемия затихла сама собой, все попытки построить жертвенник в два раза большего объема потерпели неудачу.
Еврипид в одном из своих произведений так описал задачу об удвоении куба. Царь Минос при постройке гробницы своего сына Главка объявил, что мавзолей кубической формы с длиной стороны в сто шагов слишком мал для царского сына, и повелел удвоить его объем, сохранив прежнюю форму, для чего потребовал увеличить сторону мавзолея вдвое. Минос допустил грубую ошибку: если удвоить сторону куба, то объем полученного куба будет не в два, а в восемь раз больше исходного.
Древнегреческие математики не располагали современной алгебраической нотацией и должны были решить задачу об удвоении куба исключительно при помощи циркуля и линейки. Чтобы найти сторону х квадрата, площадь которого в два раза больше площади квадрата со стороной а , они вычисляли среднее пропорциональное а и 2 а :
a / x = x /2 a , следовательно, x √2 = a
Эта же идея была применена и для решения задачи об удвоении куба. Было показано, что решение задачи сводилось к вычислению двух средних пропорциональных а и 2 а . Чтобы удвоить куб со стороной а , нужно найти сторону х куба, объем которого будет равен 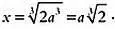
Если удастся найти значения х и у , которые будут средними пропорциональными а и 2 а согласно следующему равенству:
a / x = x / y = y /2 a
то задача будет решена. Этот метод решения, при котором исходная задача сводится к другой, более простой, весьма характерен для математики. Новая задача заключается в том, чтобы найти эти два средних пропорциональных.
Помимо задачи об удвоении куба, древнегреческих математиков интересовали и другие задачи, связанные с объемом тел. Согласно Архимеду, Евдокс доказал, что объем конуса равен трети объема цилиндра того же основания и высоты. Архимед доказал, что площадь круга равна площади прямоугольного треугольника, один катет которого равен радиусу круга, а длина другого равна длине окружности. Он также выразил объем шара через объем цилиндра и конуса.
Для этого Архимед рассмотрел полушар радиуса R и поместил рядом с ним прямой конус и прямой круговой цилиндр. Радиусы оснований конуса и цилиндра также равнялись R .
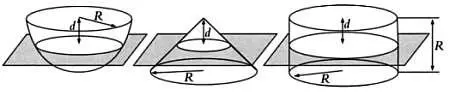
Сечения полушара, конуса и цилиндра.
Затем он рассек все три фигуры плоскостью, параллельной основанию цилиндра и расположенной на одинаковом расстоянии d от верха всех трех фигур, и рассмотрел полученные сечения. Сечением цилиндра была окружность радиуса R . Сечением полушара также была окружность, но другого радиуса (обозначим его через r ).
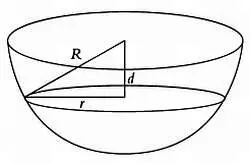
Соотношение между r, d и Rдля полушара.
По теореме Пифагора выполняется соотношение r 2+ d 2= R 2.
Сечением конуса также была окружность, но другого радиуса, d, так как угол раствора конуса составлял 45°.
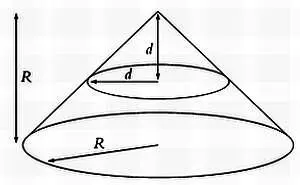
Соотношение между Rи dдля конуса.
Площади сечений таковы:
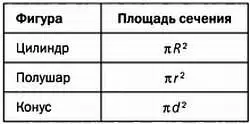
Так как r 2+ d 2= R 2, имеем:
Площадь сечения цилиндра= Площадь сечения полушара+ Площадь сечения конуса.
Сечения фигуры подобны ломтям хлеба: если для каждого сечения выполняется приведенное выше соотношение, то кажется вполне очевидным, что это же отношение будет выполняться и для объемов фигур. Иными словами,
Объем цилиндра= Объем полушара+ Объем конуса.
Архимед знал, как вычисляется объем цилиндра и объем конуса:
V (цилиндра) = πR 3; V (конуса) = 1/ πR 3.
Он получил равенство
V (полушара) = V (цилиндра) — V (конуса) = πR 3— (1/3) πR 3= 2 πR 3/3
Таким образом,
V (сфера) = 4 πR 3/3.
И вновь задачи о вычислении объемов были окончательно решены с появлением дифференциального исчисления. Рассмотрим в качестве примера, как с его помощью вычисляется объем шара радиуса г. Начнем с того, что приведем уравнение окружности
х 2+ у 2= r 2.
Вращая полукруг вокруг оси абсцисс, получим шар.
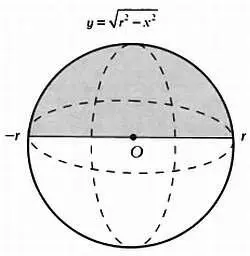
Шар, полученный вращением полукруга.
Объем тела вращения, полученного вращением плоской фигуры, ограниченной линиями у = f( x ), у = 0, х = а и х = Ь , вокруг оси ОХ , вычисляется по формуле:
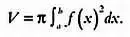
Эта формула в некотором роде отражает метод Архимеда, если интерпретировать π f( x ) 2как площадь круга и представить, что тело вращения, как в примере Архимеда, состоит из «ломтей»-сечений. Напомним, что 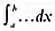 обозначает интеграл — сумму объемов бесконечного числа сечений бесконечно малой толщины ( dx ), которые составляют объем тела вращения. В нашем примере
обозначает интеграл — сумму объемов бесконечного числа сечений бесконечно малой толщины ( dx ), которые составляют объем тела вращения. В нашем примере
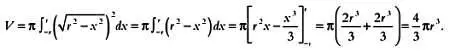
Эпилог
Интервал:
Закладка:










