Пере Грима - Том13. Абсолютная точность и другие иллюзии. Секреты статистики

Аналогичным образом при прогнозировании исходов выборов и определении степени уверенности в подобных прогнозах используются результаты предвыборных опросов и теория вероятностей. При оценке эффективности нового лекарственного препарата изучается его действие на выборке пациентов, а выводы формируются на основании полученных результатов и с помощью статистических методов, в которых применяются расчеты вероятностей.

Однако не нужно быть экспертом по теории вероятностей и необязательно уметь решать сложные задачи, чтобы понимать и применять наиболее распространенные статистические методы. Также не стоит думать, что статистика имеет отношение исключительно к азартным играм и казино. Иногда на обложках книг по статистике мы видим рулетку, игральные кости или колоду карт, хотя уместнее были бы изображения леса, операционных, школ или заводов, ведь именно в этих областях статистика имеет намного более широкое и интересное применение.

* * *

АЗАРТНЫЕ ИГРЫ И ПРОИСХОЖДЕНИЕ ТЕОРИИ ВЕРОЯТНОСТЕЙ

Теория вероятностей стоит особняком не только потому, что она появилась сравнительно поздно, но и потому, что причины ее появления и развития были достаточно необычными. Научные открытия во все времена совершались самоотверженными учеными, которые стремились понять устройство мира и часто жертвовали собой ради блага всего человечества. Однако поводом появления теории вероятностей стало желание людей, ведущих праздную жизнь, определить стратегии выигрыша в азартных играх, которым они посвящали большую часть своего времени.

Одна из первых дискуссий, посвященных математической теории вероятностей, зафиксирована в переписке Пьера Ферма с Блезом Паскалем в 1654 году. В ней речь шла о задаче, предложенной философом (и игроком!) шевалье де Мере. В задаче ставился вопрос о справедливом разделении выигрыша в неоконченной игре, если было условлено, что выигрывает тот, кто одержал верх в трех партиях, но игра завершилась со счетом 2:1.

Один из вариантов — отдать весь банк тому, кто выигрывал на момент окончания игры, другой — поделить банк поровну. Но и Ферма, и Паскаль сходились на том, что наиболее справедливым будет разделение банка в соотношении 3 к 1 в пользу того игрока, который на момент окончания игры одержал верх в двух партиях.

Обозначим игроков Аи В. А выиграл две партии. Рассуждения будут выглядеть так. Допустим, что игроки продолжают игру и вероятность победы в партии составляет 50 % для каждого из них. Возможные варианты окончания игры таковы.

1. Следующую партию выигрывает А. Так как счет станет равным 3:1, игра закончится, победу одержит А, который заберет банк. Вероятность этого исхода равна 0,5.

2. Следующую партию выигрывает В. Счет станет равным 2:2, и игра продолжится. Далее выигрывает А, счет становится равным 3:2 в пользу А, и игра завершается. Вероятность этого исхода равна 0,5·0,5 = 0,25 (выигрывает В, затем выигрывает А).

3. Следующую партию выигрывает В, затем снова выигрывает В. Игра завершается со счетом 2:3 в пользу В. Вероятность этого исхода равна 0,5·0,5 = 0,25.

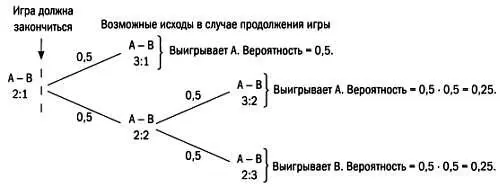
Подведем итог. Если игра продолжается, то вероятность выигрыша А будет равна 0,5 + 0,25 = 0,75, вероятность выигрыша Вбудет равна 0,25. В трех случаях из четырех побеждает А, следовательно, будет справедливо, если ему достанется три четверти банка.

* * *

В соответствии с идеями, которые высказал еще Галилей, если существует n возможных наблюдений, имеющих одинаковую вероятность, и событие А происходит в k из этих наблюдений, то вероятность события А равна:

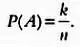
Иными словами,

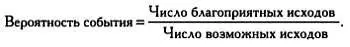
Например, если в мешке лежит 5 шаров, 3 из которых окрашены в синий цвет, а 2 — в черный, то вероятность вытащить синий шар равна 3/3. Проще не бывает.

В некоторых случаях теоретическую вероятность можно вычислить, используя симметрию объекта, от которого зависит результат, как, например, при броске монеты или игрального кубика. Другой подход заключается в том, что вероятность рассматривается как количество наблюдений, при которых произошло событие, при бесконечном увеличении числа наблюдений. Так, чтобы узнать, какова вероятность того, что при броске монеты выпадет решка, нужно бросить монету очень много раз и посмотреть, к какому значению стремится полученное соотношение исходов. Это же верно и в случае с игральными костями. Когда мы говорим, что вероятность выпадения определенного числа очков равна 1/6, мы имеем в виду идеальную игральную кость. Реальная игральная кость может отличаться от идеальной.

Некоторые исследователи бросали монету или игральную кость множество раз и записывали полученные результаты. Одним из них был английский математик Джон Керрич, который отбывал тюремное заключение в Дании во время Второй мировой войны. Находясь в тюрьме, он бросил монету 10000 раз, при этом решка выпала 3067 раз, орел — 4933.

Соотношение числа решек к числу орлов колебалось так, как показано на следующем графике, на котором приведены не реальные данные, полученные Керричем, а результаты моделирования. По мере роста числа бросков колебания уменьшаются, и разумно предполагать, что соотношение числа исходов стремится к постоянному числу при бесконечно большом числе бросков. Это значение и будет вероятностью выпадения решки при броске этой монеты.

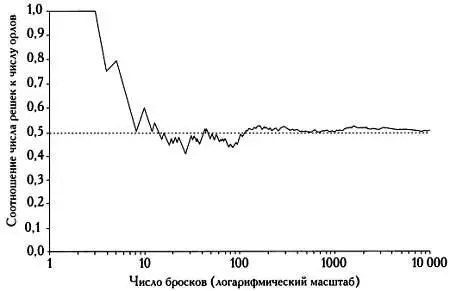
Изменение соотношения числа решек к числу орлов при броске монеты 10 000 раз (результаты получены с помощью моделирования).

Подобные исследования выполнили Жорж-Луи Леклерк де Бюффон, французский ученый XVIII века, который бросил монету 4000 раз (решка выпала 2048 раз), и Карл Пирсон, один из отцов современной статистики, который бросил монету 24000 раз (самостоятельно или с помощью ассистентов), из которых решка выпала 12 012 раз.

Жорж-Луи Леклерк де Бюффон. Портрет кисти Франсуа-Юбера Друз.