Хавьер Арбонес - Том 12. Числа-основа гармонии. Музыка и математика

* * *

КАКОВО ЧИСЛО ВСЕХ ВОЗМОЖНЫХ СЕРИЙ?

Первой нотой серии может быть любая из 12 возможных. После того как мы выбрали первую ноту, следующую можно выбрать из 11 оставшихся. Таким образом, число возможных вариантов для первых двух нот равно 12·11. Третьей нотой может быть любая из десяти оставшихся. Таким образом, число вариантов для первых трех нот равняется 12·11·10. Продолжив рассуждения, получим, что общее число возможных различных серий равно 12·11·10·9·…·3·2·1 = 479001600. Это число называется факториал 12 и записывается как 12!

Факториал любого целого положительного числа п определяется как произведение всех целых положительных чисел от 1 до n. Таким образом, n! = n·( n— 1)·…·2·1.

Однако для додекафонических серий подсчет «различных по сути» мелодий выглядит несколько сложнее, так как в этом случае не должны учитываться транспозиции, инверсии, ракоходы и сочетания этих преобразований. Тщательные подсчеты показывают, что число различных серий равно 9 985 920.

* * *

Числовая и матричная форма

Традиционные партитуры, в которых используется нотный стан, подчиняются логике диатонической музыки. Одним из следствий этого является тот факт, что расстояние между соседними линиями нотного стана и промежутками между ними не всегда обозначает один и тот же музыкальный интервал. Иногда этот интервал состоит из двух полутонов (от ре до ми ), иногда — из одного (от ми до фа ). Из-за этого в додекафонической музыке используются альтерации. По этой причине, как видно из предыдущих примеров, инверсии и ракоходы додекафонических серий «не видны» на партитурах.

Серию также можно представить в числовом виде, что упрощает запись мелодии. При записи серий в числовом виде, как правило, выбирается исходная нота. В следующем примере исходной нотой является ми , которой присвоено значение 0. Далее последовательно нумеруются полутона: фа обозначается 1, фа диез — 2, соль — 3 и так далее.

При представлении серии в числовом виде для нахождения связанных серий можно использовать средства арифметики. Например, транспозиция серии получается прибавлением одного и того же числа k к каждому элементу серии:

T k ( s 1 , s 2 , …, s 12 ) —> ( s 1 + k , s 2 + k , …, s 12 + k ),

T 0 (0, 1, 3, 9, 2, 11, 4, 10, 7, 8, 5, 6) —> (0, 1, 3, 9, 2, 11, 4, 10, 7, 8, 5, 6),

T 1 (0, 1, 3, 9, 2, 11, 4, 10, 7, 8, 5, 6) —> (1, 2, 4, 10, 3, 0, 3, 11, 8, 9, 6, 7),

T 2 (0, 1, 3, 9, 2, 11, 4, 10, 7, 8, 5, 6) —> (2, 3, 5, 11, 4, 1, 6, 0, 9, 10, 7, 8),

…

T 7 (0, 1, 3, 9, 2, 11, 4, 10, 7, 8, 5, 6) —> (7, 8, 10, 4, 9, 6, 11, 3, 2, 3, 0,1),

…

T 12 (0, 1, 3, 9, 2, 11, 4, 10, 7, 8, 5, 6) —> (11, 0, 2, 8, 1, 10, 3, 9, 6, 7, 4, 5).

После 11 счет снова начинается с 0, точно так же как мы считаем часы: 8 часов утра плюс 7 часов равно 3 часам дня. В математике подобные операции на ограниченных множествах чисел называются модулярной арифметикой. В случае с додекафоническими сериями множество чисел имеет всего 12 элементов в интервале от 0 до 11. Число элементов множества называется модулем (в нашем случае модуль равен 12). В арифметике по модулю 12 число 13 эквивалентно числу 1. Записывается это так:

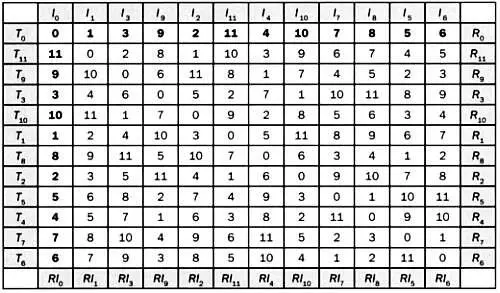
13 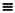1 (mod 12).

Все числа вида 12 k + 1, где k — целое, эквивалентны 1:

25 1 (mod 12),

37 1 (mod 12),

49 1 (mod 12),

61 1 (mod 12),

Как мы уже говорили, в додекафонии не проводятся различия между одинаковыми нотами, которые относятся к разным октавам. Арифметика по модулю 12 отражает этот факт: число 1, которым в нашем примере обозначена нота фа , равно 13, которым снова обозначается фа .

Средства модульной арифметики помогают заметить, что инверсия серии эквивалентна замене всех значений от 0 до 11 (то есть значений всех различных нот) разницей между этим значением и 12. При таком преобразовании значение 1 заменится на 11, 2 — на 10, 3 — на 9 и так далее. Для серии, которую мы рассматривали

в качестве примера, получим:

I ( s 1 , s 2 , .. ., s 12 ) —> ( s 1 , 12 — s 2 ,…, 12 — s 12 )

I (0,1, 3, 9, 2, 11, 4, 10, 7, 8, 5, 6) —> (0, 11, 9, 3, 10, 1, 8, 2, 5, 4, 7, 6).

Ракоход, в свою очередь, получается «обращением» числового ряда слева направо:

R ( s 1 , s 2 , ..., s 12 ) —> ( s 12 , s 11 , ..., s 1 )

R (0, 1, 3, 9, 2, 11, 4, 10, 7, 8, 5, 6) —> (6, 5, 8, 7, 10, 4, 11, 2, 9, 3, 1, 0).

Исходная серия вкупе с ее инверсией, ракоходом и с 12 возможными транспозициями для каждого из этих преобразований формирует 4·12 = 48 перестановок, которые может использовать композитор. Если учитывать повороты, то число вариантов возрастет до 48·12 = 576.

Эти 48 форм можно записать в виде матрицы размером 12 x 12, опираясь на следующие правила:

— в первой строке T 0 записывается исходная серия (в нашем примере выделена жирным шрифтом);

— в первом столбце I 0 записывается инверсия серии (также выделена жирным);

— в каждой из оставшихся ячеек записывается сумма (по модулю 12) чисел, с которых начинаются соответствующая строка и столбец. Например, пятая строка начинается с числа 10, четвертый столбец с числа 9, следовательно, на пересечении этой строки и этого столбца необходимо записать число 7, так как 10 + 9 = 19 7 (mod 12).

12 строк матрицы будут содержать исходную серию со всеми возможными транспозициями, 12 столбцов — инверсию исходной серии со всеми возможными транспозициями. Ракоходы этих 24 серий можно получить, если изменить направление обхода матрицы: строки нужно читать справа налево, столбцы — снизу вверх.

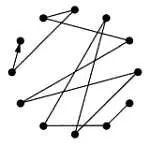
Круговая форма

Представление серии в форме круга особенно полезно при изучении додекафонии. Например, в круговой форме серия из ор. 25 Шёнберга выглядит так:

Чтобы получить ракоход серии, нужно всего лишь изменить направление обхода на противоположное:

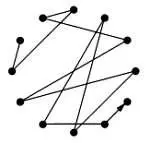
Чтобы получить инверсию серии, достаточно отобразить ее симметрично самой себе относительно оси, проходящей через основной тон:

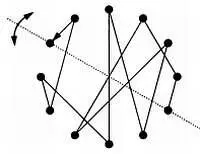
Для транспозиции нужно повернуть круг на необходимое число «часов»:

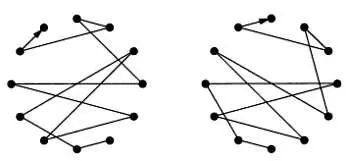
Инверсию транспозиции можно получить отражением относительно нужной оси: