Сергей Труфанов - Наука логики Гегеля в доступном изложении

Математическое умозаключение – это как раз то, чем всегда занималась и продолжает заниматься формальная логика. Это – соотношение истинных и ложных посылок умозаключения и вытекающего из них вывода. Причём определение истинности здесь вообще не подходит, поскольку, как мы выше видели, мыслить что-либо в его истине, значит мыслить, исходя из его понятия. Здесь же ни о каком понятии вообще речи нет, поскольку нет ни всеобщего, ни особенного, ни единичного. Их специфика снята и превращена в универсальные символы. Поэтому здесь речь можно вести лишь о правильности соотношения посылок умозаключения с его выводом, но никак не об их истинности.

Например: если А = В и С = В, то А = С. Если А не равно В, а С = В, то А не равно С. Если А не равно В и С не равно В, то А может быть равно, а может быть и не равно С. И т.д. Лейбниц путём комбинаций нашёл, что число таких возможных сочетаний равно 2048 формам, которые сводятся к 24 общеупотребительным формам. Но содержат ли какую-либо познавательную ценность эти формы? Этот вопрос в формальной логике задавать не принято.

§ 189. б) Благодаря тому, что посредством трёх фигур умозаключений наличного бытия была выявлена качественная однородность всех определений понятия, мышление может позволить себе теперь без оглядки на какие-либо другие качественные особенности субъекта (спортсмен, семьянин, нумизмат) перейти на ступень постижения различий внутри выявленной им абстрактной всеобщности субъектов. Что такое вуз ? – Это довольно абстрактная всеобщность, охватывающая собой всех студентов вообще. Но в пределах этой всеобщности есть существенные различия. Одни студенты получают техническое образование, другие – медицинское, третьи – педагогическое, четвёртые – фундаментальное, и т.д. Следовательно, одни из них учатся в политехническом институте, другие - в медицинском, третьи - в педагогическом, четвёртые - в классическом университете и т.д. Вузов , стало быть, много, и во всех обучаются свои студенты. Посредством умозаключений наличного бытия мы зафиксировали лишь наличное бытие вузов вообще, но ещё не их существенное различие. Установление различий между ними выводит нас на ступень умозаключений рефлексии .

Умозаключения рефлексии

§ 190. Умозаключения рефлексии по своему объективно-логическому значению соответствуют второй фигуре: В – Е – О, где серединой являются единичности . Единичности различаются между собой по своим свойствам. Одни студенты получают фундаментальное образование, другие –медицинское, третьи – техническое. По этим параметрам они отличаются друг от друга и по ним же они обособляются в конкретные всеобщности, имеющие уже вполне объективное существование ( классический университет, политехнический институт, медицинский институт).

а) Когда ряд единичных субъектов обладает каким-то одним особенным свойством, тогда мы имеем умозаключение совокупности ( общности ). Его форма: Е – О – В или, наоборот, В – О – Е. (Местоположение крайних членов, как мы уже говорили, роли не играет.) Например: Иванов получает фундаментальное образование . – Все те, кто получает фундаментальное образование, являются студентами классического университета. – Следовательно, Иванов – студент классического университета.

Умозаключение совокупности имеет следующий недостаток: всё то, что утверждается в его выводе, уже содержится в его большой посылке. ( Все те, кто получает фундаментальное образование являются студентами классического университета . Все те, кто получают медицинское образование, являются студентами мединститута ). Но чтобы утверждать, что какое-то определённое свойство присуще всем , этому надо прежде получить подтверждение. Поэтому умозаключение совокупности с необходимостью отсылает нас к умозаключению индукции .

б) Форма у мозаключения индукции : В – Е – О. Это умозаключение приводит мысль от констатации единичных случаев к утверждению общего вывода. Пример: Иванов – студент классического университета, Петров – студент классического университета, Сидоров – студент классического университета, ... и т.д. – Иванов получает фундаментальное образование, Петров получает фундаментальное образование, Сидоров получает фундаментальное образование, ... и т.д. – Следовательно, все студенты классического университета получают фундаментальное образование.

Фигура индуктивного умозаключения имеет следующий вид:

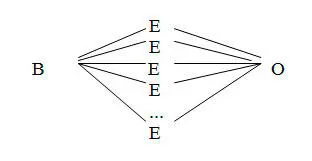
Однако единичные примеры в индуктивном умозаключении никогда не могут быть исчерпаны полностью, поэтому индукция приводит мышление к умозаключению третьей формы – аналогии , которая дополняет умозаключение индукции и компенсирует его неполноту.

в) У мозаключение аналогии (сходства). Его форма: О – В – Е, где опосредствующей серединой является всеобщее . Рассуждая по аналогии, мы основываемся на том, что все известные нам вещи одного порядка обладают некоторым свойством. Из этого мы делаем вывод, что и все другие вещи того же порядка обладают таким же свойством. Пример: Все студенты классического университета получают фундаментальное образование – Иванов является студентом классического университета – Следовательно, Иванов также получает фундаментальное образование .

Вывод из умозаключения аналогии оказывается тождественным первой посылке первого умозаключения рефлексии – умозаключения совокупности . В результате мы вновь получили сомкнувшийся круг умозаключений. Но при этом всеобщность изменила свой характер. В умозаключении совокупности мы имели всеобщность как простую полноту охвата единичных субъектов в её отличии от их других всеобщностей. Теперь же, в умозаключении аналогии , всеобщность приобрела характер объективной всеобщности. Говоря другими словами, первоначально абстрактная целокупность студентов классического университета, в её простом отличии от целокупности студентов других вузов, становится теперь целокупностью действительного классического университета из какого-нибудь города N-ска. Ну а поскольку действительный университет представляет собой уже не абстрактную, а реально существующую всеобщность, причём существующую в качестве самой себя как всеобщности, постольку теперь именно эта объективная всеобщность становится средним членом умозаключения, связующим особенное и единичное, как свои подчинённые моменты. Благодаря этому мышление переходит на ступень умозаключений необходимости.