Георг Гегель - Наука логики. Том I. Объективная логика

Во-первых, + a и – a суть противоположные величины вообще : а есть лежащая в основании обоих в-себе-сущая единица , которая безразлична к самому противоположению и служит здесь без всякого дальнейшего понятия мертвой основой. Правда, – a означает отрицательное, + a — положительное, но каждое из них есть столь же противоположное, как и другое .

Далее, а есть не только простая , лежащая в основании единица, но как + а и – а, она есть рефлексия этих противоположных в себя; имеются два разных а , и безразлично, какую из них обозначают, как положительное или отрицательное; оба обладают самостоятельным устойчивым наличием и положительны.

Взятые с той первой стороны 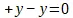; или в – 8 + 3 три единицы положительные в 3, отрицательны в 8. Противоположные упраздняются в своем соединении. Если проделан час пути на восток, и точно такой же путь обратно на запад, то последний путь упраздняет первый; сколько есть долгов, на столько меньше имущества и сколько есть имущества, столько вычеркивается долгов. Вместе с тем ни час пути на восток не есть сам по себе положительный путь, ни путь на запад не есть сам по себе отрицательный путь; а эти направления безразличны к сказанной определенности противоположности; лишь некоторое третье, имеющее место вне их соображение делает одно из этих направлений положительным, а другое отрицательным. Равным образом и долги не суть отрицательное сами по себе; они таковы лишь по отношению к должнику; для заимодавца они суть его положительное имущество; это — некоторая сумма денег (или чего бы то ни было, обладающего известной ценностью), которая становится долгом или имуществом по соображениям, имеющим место вне ее.

Противоположные, правда, упраздняют себя в своем соотношении, так что результат равен нулю; но в них имеется равным образом и их тождественное соотношение , безразличное в самой противоположности; таким образом, они составляют одно . Как было упомянуто о сумме денег, она есть лишь одна сумма, или а есть лишь одно а и в + а и в – а ; равным образом, упомянутый выше путь есть лишь один отрезок пути, а не два пути, — один на восток, а другой на запад. Точно так же и ордината у —одна и та. же, на какой бы стороне оси мы ее ни взяли; в этом смысле 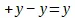; она только ордината как таковая; имеется только одно определение и один закон ординаты.

Но, далее, два противоположных суть не одно безразличное, а два безразличных . А именно, они, как противоположные, суть также и рефлектированные в себя, и таким образом остаются разными.

Так, в выражении 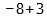дано вообще 11 единиц; + y и – у суть ординаты на противоположных сторонах оси, на которых каждая есть наличное бытие, безразличное к этой границе и в своей противоположности; таким образом, 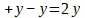.— Равным образом, путь, проделанный на восток и на запад, есть сумма двойного усилия или сумма двух периодов времени. Точно так же в политической экономии определенное количество денег или ценностей есть как средство существования не только это одно количество, а оно удвоено; оно есть средство существования и для заимодавца, и для должника. Государственное имущество исчисляется не только, как сумма наличных денег и других недвижимых и движимых ценностей, имеющихся в государстве, и тем паче, не как сумма, остающаяся свободной после вычитания пассивного имущества из активного; а капитал, хотя бы его активное и пассивное определение сводились к нулю, остается, во-первых , положительным капиталом, как 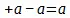; во-вторых же, поскольку он самым различным образом является пассивным капиталом, дается и снова дается в заем, он оказывается благодаря этому, весьма многообразным средством.

Но противоположные величины суть не только, с одной стороны, просто противоположные вообще, а, с другой, реальные или безразличные. Дело обстоит так, что хотя само определенное количество есть безразлично ограниченное бытие, мы все же встречаем в нем также и положительное в себе и отрицательное в себе. Например, а , поскольку оно не имеет знака, считается за положительное, если перед ним требуется поставить знак. Если бы оно должно было посредством знака стать лишь противоположным вообще, то его одинаково можно было бы принять и за – а . Но положительный знак дается ему непосредственно, так как положительное само по себе имеет своеобразное значение непосредственного, как тождественного с собой, в отличие от противоположения.

Далее, когда положительные и отрицательные величины складываются или вычитаются, то они принимаются за сами по себе положительные и отрицательные, а не за становящиеся такими лишь внешним образом через отношение сложения и вычитания. В выражении 8 – (– 3) первый минус противополагается восьми, а второй минус (– 3) есть противоположный в себе , вне этого отношения.

Ближе обнаруживается это в умножении и делении; здесь положительное следует брать по существу, как непротивоположное , отрицательное же, как противоположное, а не принимать обоих определений одинаково лишь за противоположные вообще. Так как учебники при доказательстве правил о знаках в обоих этих действиях не идут дальше понятия противоположных величин вообще, то эти доказательства страдают неполнотой и запутываются в противоречиях. — Но плюс и минус в умножении и делении получают более определенное значение положительного и отрицательного в себе, так как взаимное отношение множителей, заключающееся в том, что они суть по отношению друг к другу единица и численность, не есть просто отношение увеличения и уменьшения, как при сложении и вычитании, а имеет качественный характер, вследствие чего плюс и минус тоже получают качественное значение положительного и отрицательного. — Если не принимать во внимание этого определения и исходить только из понятия противоположных величин, легко можно вывести ложное заключение, что если 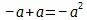, то наоборот 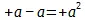. Так как один из множителей означает численность, а другой—единицу, причем за первую принимается обыкновенно первый множитель, то оба выражения 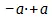и 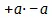различаются тем, что в первом + а есть единица и – а численность, а во втором наоборот. По поводу первого обыкновенно говорят, что если + а должно быть взято – а раз, то я беру + а не просто а раз, а вместе с тем противоположным ему образом, т. е. 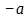раз 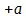(80) поэтому, так как мы имеем тут + а , то его следует брать отрицательно, и произведение есть 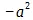. Если же во втором случае – а должно быть взято + а раз, то это – а равным образом следовало бы брать не – а раз, а в противоположном ему определении, именно + а раз. Следовательно, рассуждая, как и в первом случае, произведение должно было бы быть 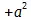. — То же самое должно было бы иметь место и при делении.