Валентин Асмус - ЛОГИКА
- Название:ЛОГИКА
- Автор:
- Жанр:
- Издательство:ОГИЗ
- Год:1947
- Город:Москва
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Валентин Асмус - ЛОГИКА краткое содержание
Предлагаемая книга представляет систематическое изложение учений логики. Она может быть использована студентами высших учебных заведений, аспирантами научно-исследовательских институтов и лицами, приступающими к самостоятельному изучению логики. Преподаватели логики в средней школе найдут в ней подробное освещение вопросов, входящих в программу их предмета, но лишь кратко излагаемых в учебниках логики для старшего класса.
ЛОГИКА - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Умозаключение по модусу ААА первой фигуры силлогизма постоянно применяется и в практике повседневного мышления. Модус этот применяется всюду там, где на основе известного знания или положения, имеющего общее значение, указываются особые , или частные , методы, пригодные для достижения цели. Так, зная общее свойство удобрений повышать урожайность и зная, что апатиты представляют один из видов удобрения, хозяйственник применяет апатиты в земледелии.
С целью облегчить запоминание правильных модусов, каждый правильный модус обозначается особым искусственным, т. е. специально придуманным, латинским словом, в котором первая гласная означает качество и количество большей посылки, вторая гласная — качество и количество меньшей посылки, а третья гласная — качество и количество вывода. Названия модусов первой фигуры следующие:
Barbara, Сelarent, Darii, Ferio.
Вторая фигура и её особые правила
§ 33.Перейдём к рассмотрению второй фигуры простого категорического силлогизма:
Р—М
S—M
———
S—Р
Вывод по второй фигуре устанавливает, что предметы класса S не могут принадлежать к классу Р, так как они не обладают свойствами, которые принадлежат предметам класса Р и которые удостоверяются в посылках.
Рассмотрим примеры:
| Все герои способны подчинять личное общественному. | Ни одна звезда не имеет быстрого видимого движения относительно других светил. | |
| Ни один эгоист не способен подчинять личное общественному. | Все планеты имеют быстрое видимое движение относительно других светил. | |
| ————————— | ———————————— | |
| Ни один эгоист не есть герой. | Ни одна планета не есть звезда. |
Примеры эти представляют две разновидности второй фигуры силлогизма. В первом примере бо́льшая посылка удостоверяет, что известное свойство М принадлежит всем предметам, входящим в класс Р, а меньшая посылка устанавливает, что предметы класса S не обладают свойством М. Из этого отношения терминов следует вывод, что ни один предмет класса S не может входить в класс предметов Р.
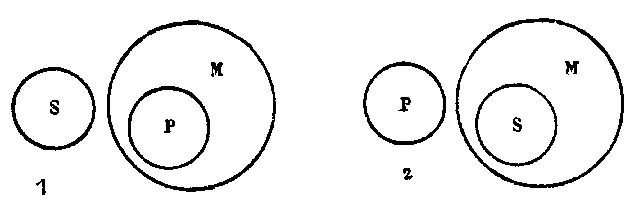
Рис. 62
Во втором примере бо́льшая посылка удостоверяет, что ни один предмет класса Р не обладает свойством М, а меньшая посылка устанавливает, что все предметы класса S обладают свойством М. Из этого отношения терминов следует, что ни один предмет класса S не может входить в класс предметов Р (см. рис. 62).
На рисунке изображено отношение между понятиями в обоих наших примерах второй фигуры. Из рисунка видно, что в обоих примерах вывод приводит к исключению класса предметов S из класса предметов Р и наоборот.
Но это исключение объёма одного понятия из объёма другого возможно только потому, что, как видно из посылок, существенные признаки обоих понятий, образующие их содержание , оказались несовместимыми.
В первом случае (1) бо́льшая посылка удостоверяет, что все существенные признаки понятия М входят как часть в число существенных признаков понятия Р и потому весь объём Р оказывается частью объёма М. Меньшая посылка удостоверяет, что существенные признаки понятия S несовместимы с существенными признаками понятия М. Но так как все существенные признаки понятия М входят в число существенных признаков понятия Р, то, будучи несовместимыми с существенными признаками М, существенные признаки S и подавно несовместимы с существенными признаками Р. А отсюда следует, что весь объём S находится вне всего объёма Р.
Во втором случае (2) бо́льшая посылка удостоверяет, что существенные признаки понятия Р несовместимы с существенными признаками понятия М и потому весь объём Р находится вне всего объёма М. Меньшая посылка удостоверяет, что все существенные признаки понятия М входят как часть в число существенных признаков понятия S и потому весь объём S есть часть объёма М. Но так как все существенные признаки М входят в число существенных признаков S, то, будучи несовместимы с существенными признаками М, существенные признаки Р будут несовместимы также и с существенными признаками S. А это значит, что весь объём S будет вне всего объёма Р.
Общим для обоих примеров является то, что в них вывод состоит в исключении предмета из класса на основании установленного посылками отличия свойств предмета от свойств класса.
§ 34.Этим значением второй фигуры определяются её особые правила. Согласно первому из них, бо́льшая посылка должна быть суждением общим. И действительно, исключить предмет S из класса предметов Р, основываясь при этом на свойствах предмета S, можно лишь при условии, если все предметы класса Р обладают свойством, противоположным свойству предмета S.
Чтобы исключить класс планет из класса звёзд, основываясь на свойстве планет иметь быстрое видимое движение относительно других светил, необходимо знать, что все звёзды обладают противоположным свойству планет свойством: не имеют быстрого видимого движения относительно других светил. Чтобы исключить класс эгоистов из класса героев, основываясь на неспособности эгоистов подчинять личное общественному, необходимо знать, что все герои обладают противоположным свойству эгоистов свойством: способны подчинять личное общественному.
§ 35.Согласно второму специальному для второй фигуры правилу, одна из посылок должна быть отрицательной. При отсутствии отрицательной посылки, посредством которой выясняется несовместимость свойства предмета и свойств предметов класса, не будет достаточного основания для исключения предмета из класса. Но какая именно из посылок — бо́льшая или меньшая — должна быть отрицательной, правило не указывает. Так, в нашем первом примере отрицательна меньшая посылка, бо́льшая же утвердительна. Во втором примере, наоборот, отрицательна бо́льшая посылка, меньшая же утвердительна. И действительно, исключение предмета из класса может основываться как на том, что предмет S не обладает свойством М, необходимо принадлежащим всем предметам класса Р, так и на том, что ни один предмет класса Р не обладает свойством М, необходимо принадлежащим предмету S. В первом случае отрицательной будет меньшая посылка, во втором случае — бо́льшая.
По второй фигуре могут быть получены только отрицательные выводы. Черта эта следует из основного назначения второй фигуры, состоящего в том, что в выводе предмет S исключается из класса предметов Р.
Отрицательные выводы могут быть получены не только по второй фигуре. Выше мы уже убедились, что из четырёх возможных правильных модусов первой фигуры два (Celarent и Ferio) также дают отрицательные выводы: общеотрицательный и частноотрицательный. С другой стороны, в дальнейшем мы убедимся в том, что и по третьей фигуре возможны отрицательные выводы.
Читать дальшеИнтервал:
Закладка:









