Авенир Уемов - Логические ошибки. Как они мешают правильно мыслить

Общеотрицательное суждение «ни одно S не есть P » выражает отношение полного исключения объемов двух понятий «ни один дельфин не есть рыба»; как видим на рис. 4, ни одна точка S не входит в P , и ни одна точка P не совпадает ни с одной точкой S .

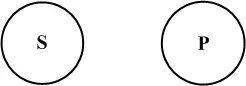
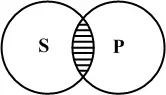
В частноутвердительном суждении «некоторые S есть P » выражается отношение частичного совпадения между объемами субъекта и предиката, как например в суждении «некоторые студенты нашей группы досрочно сдали все экзамены». Если одним кругом изобразить всех студентов нашей группы, а другим — всех студентов, сдавших досрочно экзамены, тогда студенты нашей группы, сдавшие досрочно экзамены, должны занять часть того и другого круга, что можно изобразить в виде схемы (рис. 5).

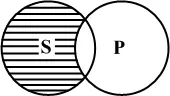
Такой же схемой выражается и частноотрицательное суждение «некоторые S не есть P », как например «некоторые студенты нашей группы не сдавали экзамены досрочно». Если одним кругом обозначить студентов нашей группы, другим — студентов, сдававших досрочно, тогда заштрихованная часть круга будет обозначать студентов нашей группы, не сдававших досрочно (рис. 6).

Частноотрицательное суждение отличается от частноутвердительного, как мы видим, тем, что в первом часть S включается в P , во втором же имеет место исключение части S из P .

В тесной связи с отношением понятий по объему находится очень важное понятие распределенности терминов в суждении. Терминами суждения называются его субъект и предикат .

Если в суждении идет речь обо всем объеме субъекта и предиката, тогда эти термины считаются распределенными. Если же говорится лишь по крайней мере о части субъекта или предиката, тогда считают, что термины не распределены. В общеутвердительном суждении «все S есть P » обо всех предметах, обозначаемых понятием S , говорится, что они включаются в объем P . Все S совпадают с P . Но мы не можем сказать, что все P включаются в объем S . Итак, в общеутвердительном суждений субъект распределен, а предикат не распределен.

В частноутвердительном суждении «некоторые S есть P » речь идет не обо всех S , а лишь о части их. Здесь часть S совпадает с частью P .

Следовательно, здесь оба термина суждения являются нераспределенными. В общеотрицательном суждении «ни одно S не есть P » обо всех S говорится, что они исключаются из P , причем исключаются они не из части P , а из всего P . Следовательно, оба термина суждения в данном случае распределены. Наконец, в частноотрицательном суждении «некоторые S не есть P » по крайней мере часть объема S исключается из объема P , следовательно, S не распределено. Но эта часть S исключается не из части, а из всего объема P , следовательно, P в данном случае распределено. Чтобы это соотношение стало еще яснее, можно сопоставить данное суждение с общеотрицательным. В чем различие между общеотрицательным и частноотрицательным суждениями? Только в субъекте. Предикат же одинаков в том и другом случае. Поэтому, если предикат в одном из этих суждений распределен, он будет распределен и в другом.

Суммируя все то, что здесь сказано о распределенности терминов, можно сделать два важных общих вывода:

1) субъект всегда распределен только в общих суждениях;

2) предикат всегда распределен только в отрицательных суждениях.

Во всех рассмотренных выше суждениях субъект и предикат не расчленялись и каждый из них мыслился как единое целое. Но возможны и суждения другого типа, когда субъект и предикат охватывают не одно, а два или более понятий. Например, «Петя станет или поэтом, или ученым». Здесь предикат «станет или поэтом, или ученым» состоит из двух самостоятельных понятий «станет поэтом», «станет ученым».

Такие суждения с расчлененным предикатом или субъектом называются разделительными . Само название указывает на расчленение здесь терминов суждения.

Союз «или», соединяющий разные части предиката в разделительном суждении, может употребляться в двух значениях:

1) неисключающее «или», когда в суждении « S есть или P 1или P 2или P 3» S может в принципе обладать одновременно всеми этими предикатами. Например, Петя может стать и поэтом, и писателем, и ученым. Суждения, в которых «или» имеет такой смысл, называются соединительно-разделительными ;

2) исключающее «или», когда в суждении « S есть или P 1или P 2или P 3» субъект обладает только одним из этих трех предикатов, например: «эта птица — или ворона, или сорока, или галка».

В этом случае «или», конечно, исключает каждый из этих 3 предикатов из двух других. Такие суждения называются исключающе-разделительными .

Исключающе-разделительное суждение может быть преобразовано в другой вид. Смысл этого суждения в том, что если S есть P 1, то S не есть P 2или P 3: если эта птица — ворона, значит, эта птица не сорока и не галка. В полученном суждении имеется условие, в котором истинность одной части обусловливает истинность другой части, в котором первая часть — основание , вторая часть — следствие , вытекающее из этого основания. Такие суждения называются условными . Условные суждения могут быть получены, таким образом, путем преобразования разделительных суждений.

В нашем примере в обеих частях условного суждения — и в основании, и в следствии — одно и то же S (птица), связки же разные: в основании — утвердительная, в следствии — отрицательная. Но это лишь частный случай условных суждений. Возьмем, например, суждение «если мороз усилится, то река замерзнет». В этом суждении субъект основания (мороз) не совпадает с субъектом следствия (река), а связка в той и другой части суждения положительная. Такой тип суждения является наиболее характерным для условных суждений. Путем различных преобразований в формулах суждений получим общий вид условного суждения.

Пусть даны два разделительных суждения, у которых будут общими один из субъектов и один из предикатов:

S 1есть или P 1, или P 2;

S 1или S 2есть P 2.

Преобразуем эти разделительные суждения в условные: