Michael A. de Budyon - БИТВА ЗА ХАОС

Попытаемся, насколько это возможно, в общих чертах объяснить что именно предложил фон Нейман, тем более что сейчас в компьютерной технике разбираются многие, а её основы преподают даже в неспециализированных университетах. [290]Итак, компьютер производит обработку данных представленных в двоичной форме, т. е. в виде логических единиц и нулей. Логическая единица или логический ноль — это просто уровни напряжения, низкий (около 0 вольт) при «нуле» и «высокий» (примерно 2,4 В) при «единице». Это называется двоичной логикой или булевой алгеброй, её аппарат был разработан в середине XIX века англичанином Д. Булем. В ней числа переводятся в двоичный код по специальной формуле, а затем все операции над ними проводятся именно в двоичном коде. Элементарных операций над логическими числами всего лишь три: дизъюнкция или сложение (ИЛИ), конъюнкция или умножение (И) и инверсия или отрицание (НЕ). Каждую из этих операций реализует т. н. логический элемент и из этих элементов можно получить такие более сложные звенья как триггеры, счетчики и регистры (они осуществляют переключение, счет и хранение логических кодов); шифраторов и дешифраторов (преобразовывают коды); мультиплексоров и демультиплексоров (коммутируют шины данных). Эта техника называется цифровой и составляет один из самых интересных разделов электроники. Ни в коем случае не подумайте, что я вам здесь рассказываю какие-то сложные и заумные вещи, понятные только подготовленным профессионалам. В Советском Союзе, в 70-80-е годы, книги по цифровой электронике издавались даже для детей среднего школьного возраста и эти дети поразительно быстро вникали во все её базовые аспекты, сами проектировали логические схемы (это очень развивает мышление — говорю вам как один из таких бывших детей). Знавал я и карапузов младшего школьного возраста, которые также всё легко «схватывали». Ну да, это вам не «Война и Мир» и не какой-нибудь Бальзак с Гюго. А потом и реализовывали схемы в «железе». Именно такие малолетки «среднего и старшего школьного возраста» одними из первых в СССР обзавелись в конце 80-ых годов компьютерами самостоятельно изготовленными на базе процессоров I8080 или Z80, в то время как почти всё взрослое население не имело о компьютерной технике ни малейших представлений. [291]К сожалению, их невообразимый потенциал был слит в 90-ых годах, либо перешел к врагам — американцам. Так что если вам будет нечего делать, можете почитать детские советские книжки по цифровой технике и двоичной логике, список смотрите в примечании.

Да, так вот, любой, даже самый сложный компьютер может быть выстроен из множества логических элементов, разумеется соединенных специальными образом. К примеру вам нужно сложить числа 5 и 2. Двоичный код числа 5 — 101, а код числа 2 — 010. И там и там — три разряда. У нас 3 разряда, поэтому берем 3 логических сумматора (элемента ИЛИ) с двумя входами (так как складываем два числа). Сумматор-дизъюнктор имеет два входа и один выход, а числа складывает по специальному правилу, на выходе мы получаем трехразрядный код 111 — код числа 7. Если вы хотите удостовериться правильно ли произведено сложение, то можете путем простейших операций сравнить полученный код с заранее «зашитым» в память кодом числа 7. Точно также можно вычитать, умножать или делить числа. Почему двоичная логика чрезвычайно удобна? Да потому что она позволяет свести самые сложные операции к множеству элементарных, пусть даже их и будет очень много (есть контакт — нет контакта). Наука не дает нам ответа как именно некоторые люди производят в уме весьма сложные операции, вроде умножения шестизначных чисел или извлечения с точностью до 3–4 знака корней n-ой степени из больших трансцендетных чисел, но факт: основа нашего головного мозга — нейрон, элементарная ячейка, могущая находиться в возбужденном или невозбужденном состоянии проводить слабые электрические импульсы или не проводить. Т. е. в общем случае иметь те же состояния что и логические элементы. Мы практически ничего не знаем о работе мозга вообще, но работа отдельного нейрона изучена достаточно хорошо. И совсем неудивительно что Росс Эшби был нейрофизиологом, а фон Нейман и Винер серьезно интересовались принципами работы мозга. В своей книге фон Нейман вообще постоянно перескакивает с элементов и реле на нейроны. И действительно, возьмите обычное реле. Подайте на обмотку напряжение («логическую единицу»), контакты замкнуться, лампочка загорится, «истинный» сигнал пройдет.

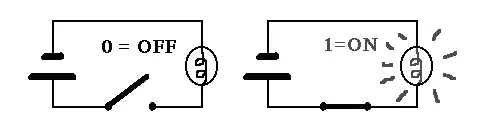
А можно сделать наоборот — при подаче напряжения реле будет не замыкать, а размыкать контакты. Т. е. при подаче «1», на выходе будет «0», а при подаче «0» (т. е. при отсутствии управляющего сигнала) на выходе будет «1». Это и есть инверсия. Неудивительно, что первые электрические вычислительные машины были собраны на реле, которые могли включаться-выключаться несколько десятков раз в секунду. Потом в них ввели электронные лампы, которые тоже «включались-выключались», но уже сотни тысяч раз в секунду. Теперь транзисторы могут делать то же самое сотни миллионов и миллиарды раз в секунду. Ну и очевидно, что если сложная вычислительная операция разбивается на множество простых и её с огромной скоростью выполняют тысячи быстродействующих элементов мы можем получить прибавку к ускорению операций во много-много порядков. А если размер быстродействующих элементов — нанометры, то вполне мощный компьютер может легко разместиться в кармане. Или в мобильном телефоне.

Но лампы и особенно реле работали крайне ненадежно в сравнении с современными комплектующими. Контакты реле залипали или наоборот обгорали, у них обламывались подвижные части, иногда они оказывались подверженными воздействию помех и т. п. Понятно, что надежность реле как элементарных звеньев стремились повысить насколько это в принципе было возможно, но этих реле были тысячи и десятки тысяч, поэтому вероятность ненадежного срабатывания всё равно была высокой, именно за счет численности. Ненадежность оказывалась неизбежностью и фон Нейман предварительно отметил что: «…ошибка рассматривается не как исключительное событие, результат или причина какой-то неправильности, но как существенная часть рассматриваемого процесса. Значение понятия ошибки в синтезировании автоматов вполне сравнимо со значением обычно учитываемого фактора правильной логической структуры которая имеется в виду». Иными словами, если мы представляем себе какими именно будут ошибки, то они не столь опасны если мы их не замечаем. Относительно вероятности ошибки вообще, он добавлял что «По убеждению автора, которого он придерживается много лет, ошибку следует рассматривать при помощи термодинамических методов, так же, как это делается с информацией в работах Сцилларда и Шеннона». Т. е. потенциально ошибаться или «срабатывать ненадежно» могут все, но с разной вероятностью.