Michael A. de Budyon - БИТВА ЗА ХАОС

Все системные процессы имеют свою геометрическую интерпретацию и такие примеры (фракталы, аттракторы, бифуркации) мы приводили. Даже картинки рисовали. Катастрофы здесь — не исключение. И если мы начали с того что привели примеры положительного восприятия сознанием арийца таких понятий как «гладкий» и «ровный», а также китайский пример уподобления жизни человека перемещению по некоему пути в пространстве-времени, то можно догадаться, что в моменты резкого роста разупорядоченности, параметры определяющие стабильность его «движения» резко изменяются и на плоскости по которой он «идет» образуются «складки» и «помятости».

Началось вроде бы с несущественных мелочей. Как обычно. В 1954 году, когда в СССР была испытана водородная бомба, а первые американские бейби-бумеры которые в наше время двинут индустрию разглаживаний, только-только вступали в пубертатный период и были совершенно «гладкими», математик Хасслер Уитни (тоже американский) опубликовал небольшую брошюру с вполне обычным названием «Об отображении плоскости на плоскость». [309]Мы её, понятное дело, пересказывать не будем, тем более что она чисто математическая и требует наличия пространственного мышления, но вкратце её суть в следующем. Нас окружают поверхности кажущиеся нам гладкими. Почему? Да потому что всё что мы видим — лишь отображение поверхностей ограничивающих предмет на сетчатку нашего глаза. Мы как бы видим не сам предмет, а его проекцию, а она плоская, т. е. гладкая. Отображения таких гладких поверхностей на плоскость мы встречаем везде, а сами эти поверхности ограничены контурами. Собственно, рисование картин — это тоже отображение трехмерных поверхностей на плоскость, в отличие, скажем, от скульптуры воспроизводящей предмет в трехмерном виде. Известно, что мужчины первым взглядом оценивают женщину именно по «контурам» ограничивающим ее «поверхности», на этом, кстати, построены многие стриптиз—шоу, где на женщину в темноте (чтоб ничего постороннего не было видно!) направляется сильный, но узконаправленный свет, именно для того чтоб выделять не выпуклые поверхности, а контура выпуклых поверхностей. О самих мужчинах можно сказать, что им свойственно не только рассматривать и возбуждаться на «контуры» женщин. Для некоторых, изменение своих собственных контуров становится идеей фикс и делом чуть ли не всей жизни, мы говорим о так называемых культуристах или бодибилдерах, этих анаболических бройлеров-андроидов современности. В теории гладких изображений так и говорится, что «видимые контуры тел — это проекции ограничивающих тела поверхностей на сетчатку глаза». Вот они и корректируют свои «видимые контуры». Впрочем, этим ещё и греки занимались, правда, стандарты «контуров» были другие.

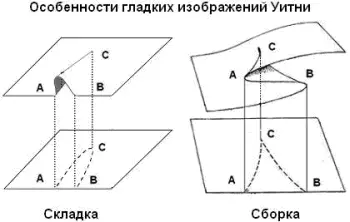
Можно привести пример попроще. Возьмите лист бумаги, без дырок и разрывов. Он — гладкий. Вы можете его аккуратно свернуть в трубочку, от этого его гладкость не пострадает. Но может случиться так, что от неаккуратного обращения лист помнется. Он уже не будет казаться нам гладким, на нем возникнут «помятости» или, как говорят математики, «особенности».

Так вот, Уитни заметил, а несколько позже и доказал (это было исключительно сложно!), что проекции на плоскость всех типов помятостей, при условии что целостность листа не нарушена (т. е. на нем нет разрывов и дырок), могут быть сведены к двум типам, названными «складкой» (fold) и «сборкой»(cusp). Более того, «складка» и «сборка» два наиболее устойчивых типа «помятостей». Могут быть и другие типы, но они легко нарушаются при незначительных шевелениях поверхности или направлениях проектирования на плоскость.

Мы уже говорили о том, как еще на заре своего существования арийцы понимали — всё имеет отношения ко всему. Возникшая позже арийская наука, как самостоятельная отрасль, отразила в себе эту модель мышления. Ученые считали и считают, что наш мир управляется неким конечным числом параметров, конечным числом законов, которые мы можем открыть, после чего будем знать о мире «всё». Эти параметры непрерывно меняются, но сам характер изменений может быть разным. Когда говорят что «всё идет гладко», имеют ввиду что параметры по которым оценивается «гладкость» меняются непрерывно, без скачков. Есть и другое выражение: «умный в гору не пойдет, умный гору обойдет». Но что такое гора? Это тоже «помятость», т. е. особенность. В предыдущей главе мы говорили про бифуркации, когда незначительные изначальные изменения параметра, например, траектории движения, могут через небольшое время привести к принципиально разным исходам. Но это т. н. «мягкие бифуркации». Гораздо интереснее в практическом плане именно катастрофы. Катастрофа — это внезапный ответ системы на ничтожное изменение окружающих условий. Вроде бы всё спокойно и все довольны, а тут раз — и получите социальный взрыв или революцию. Или стоит себе сооружение, например, московский аквапарк «Трансвааль». Он новый и кажется что простоит вечно. Внешне он производит впечатление абсолютной прочности. А потом вроде бы без всяких причин падает. В несколько секунд. Вот это пример типичной катастрофы. Есть и «восточный» пример — знаменитая поговорка про соломинку ломающую хребет верблюду, т. е. незначительное воздействие могущее вызвать фатальные последствия. Интересно, что как и в случае с фракталами и аттракторами, теория катастроф была создана французом, причем опять-таки совсем недавно.

В 1972 году Рене Том обобщил все выводы Уитни и выпустил эпохальную монографию «Structural Stability and Morphogenesis» («Структурная стабильность и морфогенезис»). [310]Он рассуждал примерно так: поскольку гладкие изображения встречаются везде, то везде должны встречаться и их особенности. Вот эти особенности и нужно использовать для изучения самых разнообразных явлений естествознания. Книга Тома была издана большим тиражом — случай невиданный со времен появления кибернетики, собственно, она и «перебила» по популярности книгу Винера. Теория катастроф — это теория скачкообразных изменений возникающих в виде неожиданного ответа системы на плавное изменение внешних условий, когда накопление мелких незначительных воздействий в конце концов вызывает лавинообразный срыв. Она дает универсальный метод исследования всех скачкообразных переходов и внезапных качественных изменений. [311]

Том выделил семь типов катастроф (опять-таки «магическое» число семь) некоторым даже дал поэтические названия: типа «ласточкин хвост», «бабочка», но нас интересует только один тип — «сборка». Она наиболее распространена и наиболее устойчива. Итак, рассмотрим конкретные примеры. Начнем с одного, отдельно взятого человека, с дискретного случая.