Феликс Филатов - КЛЕЙМО СОЗДАТЕЛЯ. Гипотеза происхождения жизни на Земле.

Возможны два варианта ответа на этот вопрос. Естественный :

— Большая Вселенная может включать в себя множество совершенно различных обширных областей, одна из которых (наша) случайно оказалась пригодной для жизни; мы не видим их, потому что горизонт каждой из них превышает десять миллиардов световых лет (для чего потребуется ввести новое понятие «скалярное поле»; для наших целей разговор о таких вещах не требуется). По существу, этот взгляд близок к концепции Мультиверса, о которой мы уже говорили.

И неестественный (или сверхъестественный ):

— То, что предыдущий вариант приписывает случайности, на самом деле — результат работы Творца, который так настроил характеристики Вселенной, чтобы они неизбежно привели квозникновению Разума в течение шести дней, каждый из которых в земной размерности составлял примерно 2 миллиарда лет.

Автор оставляет второй вариант без всяких комментариев, а «тонкая настройка» фундаментальных физических законов его не слишком занимает, поскольку она неубедительна в качестве богословского аргумента, и поскольку ее связь со структурой генетического кода — область натяжек и ничем не сдерживаемой фантазии. Справедливости ради, стоит, конечно, отметить, что знаний, накопленных сегодняшней наукой, совершенно недостаточно, чтобы обойтись без фантазиивовсе; с такой точки зрения, можно рассуждать и о Творце, и о его творениях и о гламурной суете в творческих лабораториях . Первый же взгляд на формально упорядоченные таблицы кода оставляет впечатление неслучайности его симметрий, никак не связанной с альтернативой "ключ-замок"/"замороженная случайность". Основу кодовой упорядоченности составляет молекулярная масса кодирующих и кодируемых компонентов. Мы видели, что симметричный паттерн (рисунок) канонической таблицы кода проявляется немедленно, стоит только упорядочить триплетные основания по нарастанию или убыванию их молекулярных масс. Комбинация физико-химической природы и несвязанных с ней формальных особенностей (в том числе симметрий) ключевого феномена жизни оставляет ощущение мучительной загадки. Но это ощущение усиливается многократно, когда описанные формальные особенности выражаются в терминах арифметики, и в определенных системах счисления имеют весьма характерное написание, которое в начале книжки мы даже позволили себе охарактеризовать как информационную символику .

Молекулярная масса, как основной параметр упорядочивания двух составляющих живой материи — белков и нуклеиновых кислот — играет, по-видимому, значительно большую и не слишком понятную роль в организации этих молекул, чем это принято считать. Мы уже описывали воображаемый олигопептидный фрагмент (МПП), состоящий из всех 61 кодируемых аминокислотных остатков. Равновесие масс его константного хребта и вариабельных боковых цепей трудно объяснить — проще принять за данность и свойство генетического кода. Выраженное числом нуклонов, такое равновесие впечатляет абсолютной точностью.

Симметрии полипептидных цепочек заставляют присмотреться и к цепочкам нуклеиновых кислот (полинуклеотидным). Мы уже отмечали равенство масс комплементарных пар GC и АТ , которое — к тому же — выражается все той же информационной символикой (в четверичной системе счисления, основание которой соответствует четверке оснований). Однако, в этом случае «хребет» полинуклеотида всегда тяжелее, чем его вариабельные части. Тем не менее, носители генетической информации также демонстрируют молекулярные симметрии — хотя и несколько другого характера. Одни из них гармонизированы с упомянутым равновесием комплементарных пар и называются первым правилом Чаргаффа (число G двойной спирали ДНК равно числу С этой спирали, а число А — соответственно — числу Т ): G = C , A = T . Первое правило естественно вытекает из структуры этой замечательной молекулы (в свое время оно — как раз напротив — послужило основой для понимания структуры ДНК). Два других правила Чаргаффа — второе и третье — описывают соотношения пуринов и пиримидинов в составе ДНК ( A + G = C + T или R = Y , как мы обозначаем здесь пурины и пиримидины) и вытекающее из первых двух равенство числа оснований, содержащих аминогруппы в положении 4 пиримидинового ядра и в положении 6 — пуринового ( С и А ), числу оснований, содержащих оксо-группу в тех же положениях ( G и T ): С + А = G + T ). Соотношение ( G + C ):( A + T ) называют коэффициентом специфичности, и ДНК каждого вида имеет собственный коэффициент, который колеблется от 0.3 до 2.8. Не очень давно была обнаружена еще одна закономерность, касающаяся нуклеотидного содержания ДНК. Именно эту закономерность называют сейчас вторым правилом Чаргаффа [65], поскольку перечисленные выше правила взаимозависимы (то есть составляют как бы одно ) и поскольку его начальная формулировка была абсолютно тождественна первому правилу ( G = C , A = T ). Но относилась она только к одной цепочке ДНК ! «С какой стати?» — отозвался известный ученый, когда впервые услышал об этом. Второе правило до сих пор остается загадкой и известно гораздо меньше первого. Справедливости ради следует сказать, что это правило хорошо соблюдается для разделенных поли-ДНК-цепей длиной 70-100тысяч оснований (девиация — сотые доли процента), хуже — для длин 1-10тысяч и практически не соблюдается для длин менее 100 нуклеотидов. Именно поэтому многие специалисты объявили это правило статистическим и тривиальным. В своих весьма любопытных и отлично написанных текстах в ЖЖ (http://galicarnax.livejournal.com/), названных « Подумаешь, геном Ньютона! », замечательный, но неизвестныйАвтору автор, скрывающийся под ником Galicarnax , очень внятно показывает, почему второе правило вовсе нетривиально. « Если сгенерировать длинную случайную последовательность из четырех оснований , — пишет он, — то в ней в силу статистики... количества всех четырех нуклеотидов будут примерно равны. Но в реальных геномах это не так. Там обычно либо А, либо В :

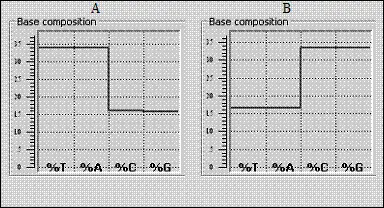
Геномы с почти равным распределением оснований — как в случайной последовательности — крайне редки ». И при этом второе правило совершенно не связано с относительным размером кодирующей части генома, поскольку " соблюдается и для ДНК человека, в которой кодирующие последовательности составляют менее 2%, и для ДНК бактерий, в которой они составляют 80-95%.Так что с белками это правило никак не связано «...Зато само по себе это правило оказалось частным случаем более общего закона, который заключается в том, что «в одной цепочке [ природной ] ДНК содержится примерно равное количество комплементарных олигонуклеотидов».