Жиль Делёз - Складка. Лейбниц и барокко

Итак, необходимость второго этажа подтверждается повсюду, собственно говоря, метафизически. Все та же душа и образует второй этаж, или интериорность верха, — ведь там у нее уже нет окна для восприятия внешних влияний. Даже в физике мы переходим от внешних материальных складок к внутренним сгибам, — спонтанным и одушевленным. Их-то теперь — как их природу,

{31}

«Разъяснение трудностей, обнаруженных г-ном Бейлем в новой системе» (GPh, IV, р. 544, 558). Геру показал, как внешний детерминизм и внутренняя спонтанность превосходно уживаются между собой — уже в отношении физических тел: р. 203–207 и р. 163 («теперь эластичность рассматривается, как выражение первичной спонтанности, изначальной активной силы»).

{32}

«Новая система Природы», § 18; «Об усовершенствовании первой философии и о понятии субстанции.»

{25}

так и способы их разгибания — и следует рассмотреть. Все выглядит так, словно складки материи не имеют оснований в самих себе. Объясняется ли это тем, что Большая Складка всегда расположена между двумя малыми и что этот «промежуток-между-складками», на первый взгляд, присутствует при всех переходах: между неорганическими телами и организмами, между организмами и животными душами, между душами животными и разумными, между душами и телами вообще?

{26}

Генетическим и идеальным элементом переменной кривой, или сгиба, является инфлексия. Инфлексия — это подлинный атом, эластичная точка. Именно ее выделил Клее в качестве генетического элемента активной и спонтанной линии, тем самым свидетельствуя о собственной близости стилю барокко и Лейбницу и противопоставляя себя картезианцу Кандинскому, для которого углы и точка являются жесткими и приводятся в движение внешней силой. Однако для Клее точка, как «неконцептуальный концепт непротиворечия», проходит через инфлексию. Это и есть сама точка инфлексии той, где кривую пересекает касательная, точка-сгиб. Клее начинает с последовательности из трех фигур. 1На первой изображена инфлексия. Вторая показывает, что не бывает фигур правильных и беспримесных, — как писал Лейбниц, «нет прямых, к которым не примешивалась бы искривленность», но как и «нет конечных кривых определенного характера, к которым не примешивались бы какие-нибудь другие — и это как в мельчайших, так и в наиболее крупных частях»; так что «ни одному телу вообще невозможно назначить определенную четкую поверхность, что можно было бы сделать, если бы у него были атомы». 2На третьей фигуре заштрихованы выпуклые стороны; тем самым выделяются вогнутости и центры их кривизны, находящиеся

1Klee, Theorie de i'art moderne, Gonthier, p. 73.

2

Письмо к Арно, сентябрь 1687 (GPh, II, р. 119).

{27}

по разные стороны кривой с каждой стороны от точки инфлексии.

Бернар Каш определяет инфлексию, или точку инфлексии, как внутреннюю сингулярность. В противоположность «экстремумам» (внешним сингулярностям, максимуму и минимуму), она не имеет координат: она не находится ни наверху, ни внизу, ни справа, ни слева; не входит ни в регрессивную, ни в прогрессивную последовательность. Скорее, точка инфлексии соответствует тому, что Лейбниц называет «двусмысленным знаком». Она находится в состоянии невесомости; кроме того, векторы вогнутости не имеют ничего общего с вектором силы тяжести, так как детерминируемые ими центры кривизны вибрируют по разные стороны кривой. Следовательно, инфлексия является чистым Событием линии или точки, Виртуальным, идеальностью по преимуществу. Когда-нибудь она попадет на оси координат, но пока она находится вне мира: она сама — мир, или начало мира, — писал Клее, — это «место космогенеза», «точка вне измерений», «промежуток между измерениями». Событие, представляющее собой ожидание события? Именно в этом качестве инфлексия и подвергается возможным трансформациям; по Кашу, бывает три типа трансформаций. 3

Фиг. 1 Та же линия с сопутствующими ей формами (фиг. 2 и 3).Bernard Cache, L'ameublement du territoire (в печати). Этот текст на географические, архитектурные и особенно меблировочные темы представляется нам обязательным для всех теорий складки. Активная, так сказать, резвящаяся в свое удовольствие линия, Прогулка ради прогулки, без определенной цели. Эту линию производит точка в движении (фиг. 1).

Фиг. 1

Та же линия с сопутствующими ей формами (фиг. 2 и 3).

Bernard Cache, L'ameublement du territoire (в печати). Этот текст на географические, архитектурные и особенно меблировочные темы представляется нам обязательным для всех теорий складки.

Фиг. 2

Фиг. 3

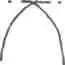Огива Готическая размеренность: огива и загиб (схема Бернара Каша)

Огива

Точка загиба

Фигуры Клее

Трансформации первого типа — векториальные или симметричные, с ортогональной или касательной плоскостью отражения. Они происходят по оптическим законам и преобразуют инфлексию в геометрическую точку загиба складки или в огиву. Огива выражает собой форму движущегося тела, чья конфигурация сливается с линиями течения жидкости, — а загиб складки

профиль дна долины, когда воды располагаются в порядке единого течения.

{29}

Трансформации второго рода — проективные: в них выражается проекция на внешнее пространство пространств внутренних, определяемых «скрытыми параметрами» и переменными величинами, или потенциальными сингулярностями. В этом смысле трансформации Тома открывают морфологию живого на основе семи элементарных событий-катастроф: складки, сборки, «ласточкина хвоста», «бабочки», а также омбилических точек: гиперболической, эллиптической и параболической. 4

Наконец, инфлексия сама по себе неотделима от бесконечного варьирования или от бесконечно переменной кривизны. Закругляя углы сообразно требованиям барокко и приумножая их по закону гомотетии (подобия), мы получаем кривую Коха, которая проходит через бесконечное количество угловатых точек и ни в одной из этих точек не допускает касательной; служит оболочкой бесконечно губчатого или полостного мира; образует более чем одну линию и менее чем одну поверхность (фрактальное измерение Мандельброта, выражаемое дробным или иррациональным числом; нон-измерение; промежуточное измерение). 5Вдобавок, гомотетия способствует совпадению вариации с переменой масштаба, как в случае с длиной берега в географии. Как только мы вмешиваем в дело флуктуацию, а не внутреннюю гомотетию, все меняется. Мы получаем уже не возможность определять угловатую точку между двумя другими, сколь бы близкими те ни были, — а свободу где угодно добавлять поворот, превращая всякий промежуток в место новой складчатости. Как раз здесь мы и переходим от сгиба к сгибу, а не от