Юрий Ивлев - Логика для юристов: Учебник.

Отношения между атрибутивными суждениями с одними и теми же терминами изображаются посредством схемы, называемой логическим квадратом:

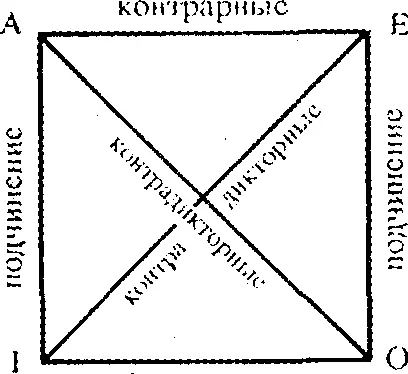
субконтрарные

Между суждениями форм А и I, а также форм Е и О имеет место отношение подчинения. Между А и Е — контрарности, а I и О — субконтрарности. Суждения логических форм А и О, а также Е и I находятся в отношении контрадикторности.

Устанавливать отношения между суждениями можно также с помощью следующей таблицы:

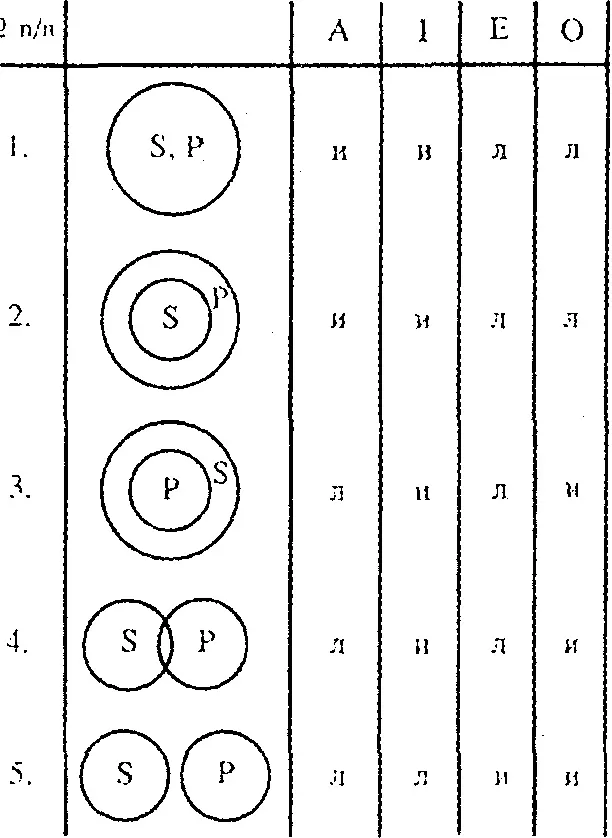
В ней указаны возможные значения истинности суждений различных видов при различных отношениях между объемами их терминов ( S и P). Например, нет строк, в которых суждения форм А и О оба имеют значение “истина”, нет таких строк, в которых оба имеют значение “ложь”. Следовательно, суждения А и О находятся в отношении контрадикторности.

Отношения между суждениями о двухместных отношениях можно изобразить при помощи логического квазишестиугольника:

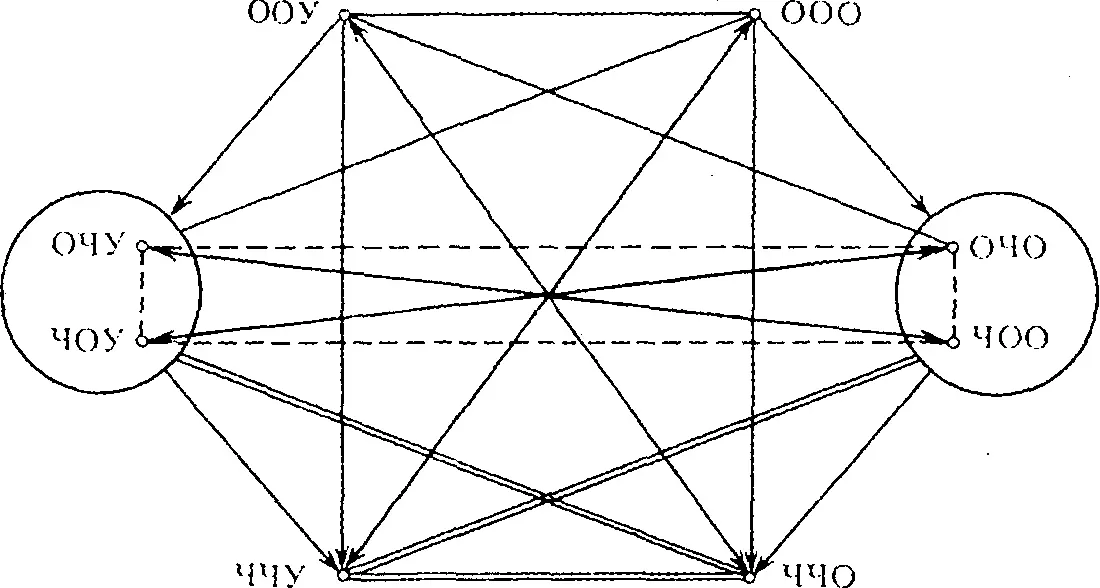
Сокращенно суждения о двухместных отношениях обозначаются словами, состоящими из заглавных букв О (общее), Ч (частное), У (утвердительное), О (отрицательное). В последнем смысле буква О понимается лишь тогда, когда она находится в конце трехбуквенного слова. Например, слово "ООО" обозначает обще-общеотрицательное суждение, слово " ЧОУ" — частно-общеутвердительное суждение и т.д.

На схеме двойной стрелкой изображено отношение контрадикторности, стрелкой — отношение подчинения, прямой — отношение контрарности, двойной линией — субконтрарности, штриховой — отношение логической независимости.

Методы установления отношений между сложными суждениями излагаются в главе V.

Упражнение 10

В каком отношении находятся суждения?

1. Если идет дождь, то крыши мокрые. Дождя нет, а крыши мокрые.

2. Некоторые юристы обладают ораторскими способностями. Некоторые юристы не обладают ораторскими способностями.

3. Если тело является кристаллическим, то оно имеет определенную температуру плавления. Данное тело не является кристаллическим, поскольку оно не имеет определенной температуры плавления.

4. Если подсудимый виновен, то у него был сообщник. Подсудимый виновен, но у него не было сообщника.

5. Если болезнь запущена, то ее легко распознать, но трудно излечить. Если болезнь не запущена, то ее трудно распознать, но легко излечить.

6. Тому, кто тратит свое, лучше всего быть бережливым. Тому, кто тратит чужое, можно быть щедрым.

7. Если человек совершил преступление и это установлено, то он подлежит привлечению к уголовной ответственности. Если человек совершил преступление, то он подлежит привлечению к уголовной ответственности. Человек совершил преступление, но не подлежит привлечению к уголовной ответственности.

Отрицание суждения — это операция, заключающаяся в таком преобразовании его логического содержания, в результате которого получают суждение, находящееся в отношении контрадикторности к исходному.

Пусть кто-то утверждает: “Все студенты нашей группы — отличники”. А кто-то не соглашается с этим и отрицает выдвинутое суждение: “Неверно, что все студенты нашей группы —отличники”. Что же верно? Какое суждение (без внешнего отрицания) является отрицанием суждения “Все студенты нашей группы — отличники”? Отрицанием является суждение “Некоторые студенты нашей группы не являются отличниками”, т.е. отрицанием общеутвердительного суждения (А) является частноотрицательное ( О ).

При отрицании атрибутивного суждения меняются его качество и количество. Отрицая общее суждение, получаем частное, и , наоборот, отрицая частное, получаем общее. Отрицая утвердительное суждение, получаем отрицательное, и наоборот, отрицая отрицательное, получаем утвердительное. Наглядно это можно представить следующим образом:

Общее суждение

Утвердительное суждение

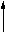
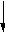
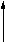
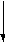
Частное суждение

Отрицательное суждение

Здесь стрелка показывает, какое суждение получается при отрицании исходного. Предположим, что мы отрицаем суждение “Некоторые люди дышат жабрами”. Это суждение частное. Стрелка показывает, что отрицанием частного суждения является общее. Отрицаемое суждение — утвердительное. Результатом отрицания утвердительного суждения является отрицательное. Следовательно, результатом отрицания исходного суждения является общеотрицательное суждение. Его структура “Ни одно S не суть Р ” . Подставляя вместо S “люди”, а вместо Р “дышащий жабрами”, получим суждение “Ни один человек не дышит жабрами”.

При отрицании суждений об отношениях их качество и количество, так же как и при отрицании атрибутивных суждений, меняются на противоположные.

Предположим, что требуется осуществить отрицание суждения “Каждый юрист знает некоторого математика”. Это суждение по качеству — утвердительное, а по количеству — обще-частное. Следовательно, в результате отрицания исходного суждения мы должны получить суждение по качеству — отрицательное, а по количеству — частно-общее. Таковым является суждение “Некоторые юристы не знают ни одного математика”.

Результатом отрицания (неопределённо) конъюнктивного суждения является дизъюнктивное суждение, в котором составляющие суждения являются отрицаниями составляющих суждений исходного конъюнктивного суждения. Предположим, что отрицается суждение “Все юристы изучают логику, и все философы изучают логику”. Результатом отрицания является суждение “Некоторые юристы не изучают логику или некоторые философы не изучают логику”.

Таким образом, отрицая суждение формы А  В, получаем суждение формы  A  В. Иначе:  (А  В)  ( А  В ).

Последовательно-конъюнктивное суждение отрицается по следующей схеме:  (A ⊤ B)   A  B  (A  B )  (B ⊤ A) .

Например, отрицанием суждения “Целесообразно ликвидировать монополию производителей, а затем целесообразно освободить цены” является суждение “Нецелесообразно ликвидировать монополию производителей или нецелесообразно освобождать цены, или целесообразно ликвидировать монополию производителей и (одновременно) освободить цены, или нужно освободить цены, а затем ликвидировать монополию производителей”.