Юрий Ивлев - Логика для юристов: Учебник.

2. Уточните и упростите условия работы автоматизированной системы управления (АСУ) при помощи алгебры логики: в противопожарных целях температура на объекте не должна превышать 40° С; для предупреждения перегрева объекта предлагается установить два вентилятора (малый и большой) и разработать АСУ, удовлетворяющую следующим условиям: при температуре ниже 20° С вентиляторы не работают, при температуре от 20° С до 30° С работает малый вентилятор, при температуре от 31° С до 36° С работает большой вентилятор, при температуре свыше 36° С работают оба вентилятора, а когда температура на объекте достигает 40° С, звучит сигнал тревоги — сирена.

Алгебра логики применяется для анализа управленческих решений. С ее помощью можно, например, найти противоречие в самом решении, установить, что решение противоречит другим решениям, ранее принятым.

Алгебра логики используется для упрощения формулировки управленческих действий, предписываемых решением.

Пусть управленческое решение устанавливает, что:

1) к патрульно-постовой службе могут привлекаться сотрудники наружной службы горрайоргана внутренних дел;

2) никто не может быть одновременно сотрудником наружной службы и оперативного подразделения, если он не привлекается к несению патрульно-постовой службы;

3) никто из личного состава оперативных подразделений не привлекается к патрульно-постовой службе.

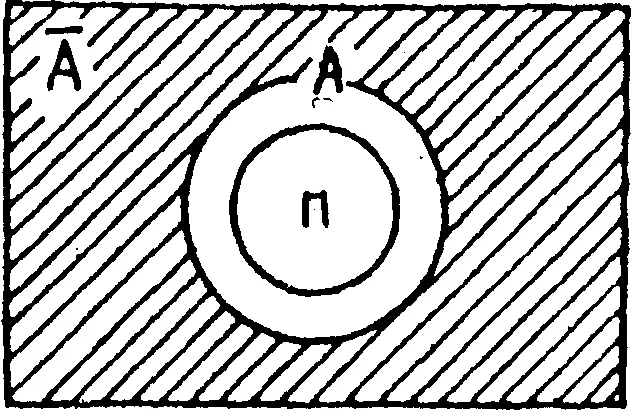
Упростим это предписание [67] См.: Беркли Э. Символическая логика и разумные машины. М., 1961. С. 51. , состоящее из трех суждений. Для этого обозначим класс сотрудников патрульно-постовой службы символом П, класс сотрудников наружной службы — А, класс сотрудников оперативного подразделения — О n.

Запишем предписание следующим образом:

_

1) все П суть А, а в виде тождества — П • А= 0, т.е. класс П включается в класс А;

_

2) все, кто есть А и О суть П, А • О n• П = 0;

3) никто из О nне есть П, О n• П = 0.

Затем преобразуем это предписание:

_

1) П • А=0 — первое суждение предписания,

_

2) П • A  0=0 — из 1) по Т6,

_ _

3) П • A  A • О n• П=0 — из 2), используя второе суждение,

_ _

4) П • А  А • О n • П  0=0 — из 3) Т6,

_ _

5) П • А  А • О nП  О n, • П=0 — из 4), используя третье суждение,

_ _ _

6) П • А  А • О n• П  (О n• П) • (A  A)=0 — из 5) на основании

_ _ _ Т6 и Т7,

7) П • A  А • О n• П  О n• П • А  О n• П • А=0 — из 6) на основании

_ _ _ Т3,

8) П • А  О n• П • А  А • О n• П  А • О n• П=0 — из 7) на основании

_ _ _ Т1,

9) П • А  П • А • О n А • О n• П  A • О nП=0 — из 8) на основании

_ _ Т1,

10) П • А  А • О n• П  A • О n• П=0 — из 9) на основании

_ Т5,

11) П • А  А • О n= 0 — из 10) на основании

Т10.

Если объединение двух классов равно 0, то каждый из этих классов равен

_

0, следовательно, П • А=0 и А • О n=0.

Получаем предписание, тождественное исходному:

1) патрульно-постовая служба формируется из состава наружной службы;

2) никто из личного состава оперативных подразделений не может быть сотрудником наружной службы.

Полученное предписание проще исходного. Если управленческие решения являются сложными, то их упрощение может быть значительным.

1. Символическая логика, в том числе алгебра логики, широко применяется в кибернетике. Об отце символической логики Лейбнице Норберт Винер, сформулировавший основные идеи кибернетики, пишет: “Если бы мне пришлось выбирать в анналах истории наук святого — покровителя кибернетики, то я выбрал бы Лейбница. Философия Лейбница концентрируется вокруг двух идей, тесно связанных между собой: идеи универсальной символики и идеи логического исчисления.

Из этих двух идей возникли современный математический анализ и современная математическая логика. И как в арифметическом исчислении была заложена возможность развития ее механизации от абака и арифмометра до современных сверхбыстрых машин, так и в исчислении умозаключений Лейбница содержится в зародыше думающая машина. Сам Лейбниц, подобно своему предшественнику Паскалю, интересовался созданием вычислительных машин в металле. Поэтому совсем неудивительно, что тот же самый умственный толчок, который привел к развитию математической логики, одновременно привел к гипотетической или действительной механизации процессов мышления” [68] Винер Н . Кибернетика. М.. 1968. С. 57. .

2. Алгебра логики применяется при проектировании переключательных схем, являющихся элементами автоматизированных систем управления и вычислительных машин. При этом символ “•” интерпретируется как последовательное соединение переключателей, а символ “” — как параллельное. Например, формулам p • (q  r ) и р • q  р • r соответствуют следующие схемы:

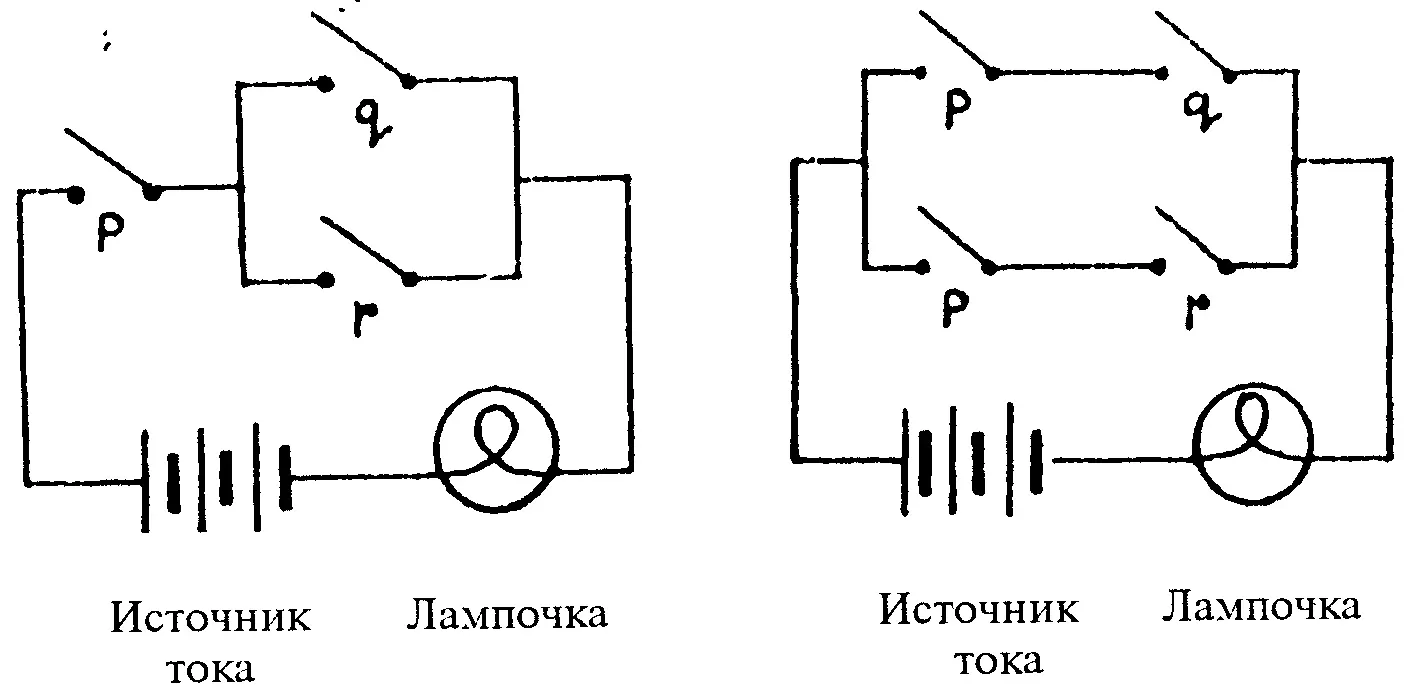
р = 1 — переключатель замкнут, р = 0 — разомкнут. Если в схеме имеются два (или более) переключателя р, то они могут быть замкнуты (или разомкнуты) только одновременно (именно поэтому они обозначаются одной и той же буквой).

По электрической цепи, изображенной на левой схеме, ток идет тогда и только тогда, когда он идет по цепи, изображенной на правой схеме, так как формулы р • (q  r ) и р • q  р • r — тождественные.

Символ “-” интерпретируется как противоположное состояние

_ _

переключателя, т.е. если р = 1, то p = 0, а если переключатель р замкнут, то p

_

разомкнут. Так, формуле р  p соответствует схема:

_

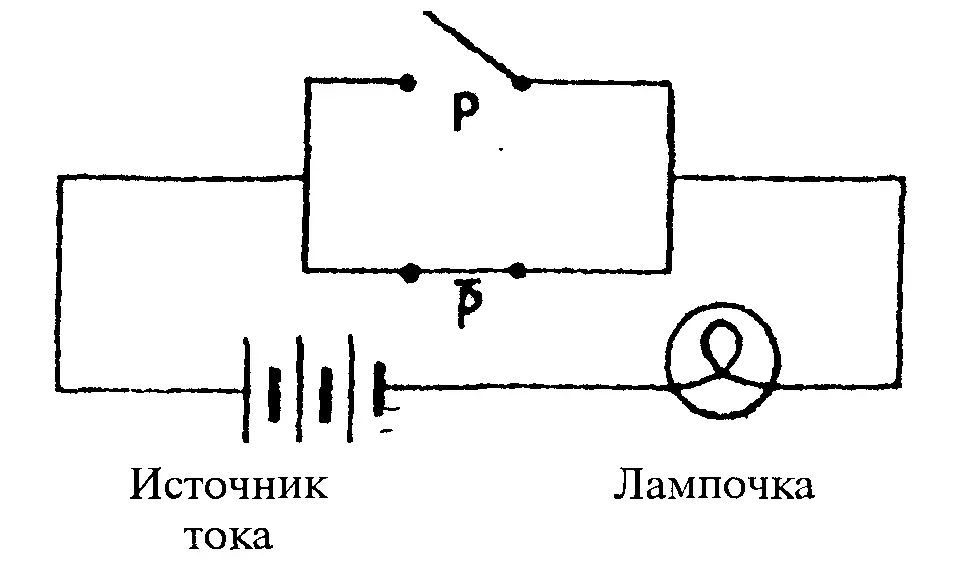
По этой цепи ток идет всегда, так как р  р = 1, т.е. если переключатель р

_

разомкнут, то переключатель р замкнут, и наоборот. Лампочка горит постоянно. Можно упростить схему, убрав оба переключателя.

Алгебра логики располагает средствами, позволяющими найти наиболее простую схему (например, содержащую наименьшее число переключателей) по сравнению с данной, но выполняющую те же функции, что и исходная.

3. “Прекрасно приспособленная для описания комбинаторных явлений, эта теория получает многочисленные применения к исследованию операций, где се нередко связывают с теорией структур.” [69] Кофман А., Фор Р. Займемся исследованием операций. М., 1966. С. 187.

Алгебра логики применяется также в сетевом планировании и линейном программировании.

4. Алгебра логики применяется при установлении правильности или неправильности рассуждении. Пример рассуждения: “Если Иванов является участником этого преступления, то он знал потерпевшего. Иванов не знал потерпевшего, но знал его жену. Потерпевший знал Иванова. Следовательно, Иванов не является участником этого преступления.” Переведем рассуждение на язык алгебры логики. Обозначим символами простые суждения, входящие в рассуждение: “Иванов является участником этого преступления” ( р ), “Иванов знал потерпевшего” ( q ), “Иванов знал жену потерпевшего” ( r ), “потерпевший знал Иванова” ( s ) . Затем переведем на язык алгебры логики посылки и