Вячеслав Кириллов - Логика: учебник для юридических вузов

направленности логического следования, по количеству посылок?

Суждение, содержащее новое знание, может быть получено посредством преобразования суждения. Так как исходное (преобразуемое) суждение рассматривается как посылка, а суждение, полученное в результате преобразования, — как заключение, умозаключения, построенные посредством преобразования суждений, называются непосредственными. К ним относятся: 1) превращение, 2) обращение, 3) противопоставление предикату.

Выводы в каждом из этих умозаключений получаются в соответствии с логическими правилами, которые обусловлены видом суждения — его количественными и качественными характеристиками.

1. Превращение

Преобразование суждения в суждение, противоположное по качеству с предикатом, противоречащим предикату исходного суждения, называется превращением.

Превращение опирается на правило: двойное отрицание равносильно утверждению : ˥˥р ≡ р, где р— любое суждение, ˥— символ отрицания, ≡— символ эквивалентности (равнозначности).

Превращать можно общеутвердительные, общеотрицательные, частноутвердительные и частноотрицательные суждения.

Общеутвердительное суждение (А) превращается в общеотрицательное (Е).

Схема превращения суждения А:

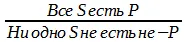
Пример:

Все сотрудники нашего коллектива ( S) — квалифицированные специалисты ( Р).

______________

Ни один сотрудник нашего коллектива ( S) не является неквалифицированным специалистом ( не-Р).

Общеотрицательное суждение (Е) превращается в общеутвердительное (А).

Схема превращения суждения Е:

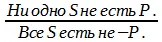
Пример:

Ни одна незаконная сделка ( S) не является действительной ( Р).

__________________

Все незаконные сделки ( S) являются недействительными ( не-Р).

Частноутвердительное суждение (I) превращается в частноотрицательное (О).

Схема превращения суждения I:

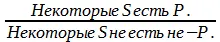
Пример:

Некоторые государства ( S) являются европейскими ( Р).

__________________

Некоторые государства ( S) не являются неевропейскими ( не-Р).

Частноотрицательное суждение (О) превращается в частноутвердительное (I).

Схема превращения суждения О:

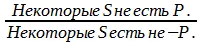
Пример:

Некоторые преступления ( S) не являются умышленными ( Р).

________________

Некоторые преступления ( S) являются неумышленными ( не-Р).

Таким образом, чтобы превратить суждение, нужно заменить его связку на противоположную, а предикат — на понятие, противоречащее предикату исходного суждения. Суждение, полученное посредством превращения, сохраняет количество, но изменяет качество исходного суждения. Субъект исходного суждения не изменяется.

Заключения, полученные посредством превращения, уточняют наши знания. Устанавливая отношения между субъектом и понятием, противоречащим предикату исходного суждения, мы рассматриваем предмет суждения с новой стороны, фиксируя внимание на признаке, не совместимом с признаком, выраженным в предикате исходного суждения. В этом смысл превращения. Поэтому заключения, полученные с помощью этой логической операции, содержат некоторые новые знания о предмете.

2. Обращение

Преобразование суждения, в результате которого субъект исходного суждения становится предикатом, а предикат — субъектом заключения, называется обращением.

Обращение подчиняется правилу: термин, не распределенный в посылке, не может быть распределен в заключении [31] О распределенности терминов в суждениях см. гл. IV, § 5. В примерах распределенность термина обозначается знаком «+», нераспределенность — знаком «—». .

Различают обращение без ограничения объема и обращение с ограничением объема.

Обращением без ограничения объема называется обращение без изменения количества суждения. Так обращаются суждения, оба термина которых распределены или оба не распределены. Если же предикат исходного суждения не распределен, то он не будет распределен и в заключении, где он становится субъектом. Поэтому его объем ограничивается. Такое обращение называется обращением с ограничением.

Общеутвердительное суждение (А) обращается в частноутвердительное (I), т. е. с ограничением. Например:

Все студенты нашей группы сдали экзамены (Р—).

______________________

Некоторые сдавшие экзамены (Р—) — студенты нашей группы.

В исходном суждении предикат не распределен, поэтому он, становясь субъектом заключения, также не распределен. Его объем ограничивается («некоторые сдавшие экзамены»).

Схема обращения суждения А:

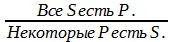
Общеутвердительные выделяющие суждения (в них предикат распределен) обращаются без ограничения, по схеме:

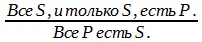
Например:

Кража (и только кража) есть тайное хищение чужого имущества ( Р+).

________________________

Тайное хищение чужого имущества ( Р+) есть кража.

Общеотрицательное суждение (Е) обращается в общеотрицательное (Е), т. е. без ограничения. Например:

Ни один студент нашей группы не является неуспевающим ( Р+).

________________

Ни один неуспевающий ( Р+) не является студентом нашей группы.

Это суждение обращается без ограничения, потому что его предикат («неуспевающие») распределен.

Схема обращения суждения Е:

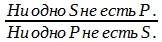
Частноутвердительное суждение (I) обращается в частноутвердительное (I). Это обращение без ограничения. Предикат, не распределенный в исходном суждении, не распределен и в заключении. Количество суждения не изменяется. Например:

Некоторые студенты нашей группы — отличники (Р—).

________________________

Некоторые отличники (Р—) — студенты нашей группы.