Вячеслав Кириллов - Логика: учебник для юридических вузов

Например, из посылок «Студенты нашего института ( М) не изучают биологию ( Р)», «Сотрудники НИИ ( S) не являются студентами нашего института ( М)» нельзя получить необходимого заключения, так как оба крайних термина ( Sи Р) исключаются из среднего. Поэтому средний термин не может установить определенного отношения между крайними терминами. В заключении меньший термин ( М) может полностью или частично входить в объем большего термина (Р ) или полностью исключаться из него. В соответствии с этим возможны три случая: 1) «Ни один сотрудник НИИ не изучает биологию ( S 1 ); 2) «Некоторые сотрудники НИИ изучают биологию» ( S 2 ); 3) «Все сотрудники НИИ изучают биологию» ( S 3 ) (схема 34).

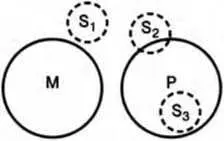
Схема 34

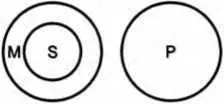
Схема 35

б) Если одна из посылок — отрицательное суждение, то и заключение должно быть отрицательным.

Например:

Судья, являющийся родственником потерпевшего ( М), не может участвовать в рассмотрении дела ( Р).

Судья К. — родственник потерпевшего ( М).

____________________

Судья К. ( S) не может участвовать в рассмотрении дела ( Р).

Этот пример показывает, что в силлогизме с одной отрицательной посылкой средний термин исключается из объема крайнего термина (в данном случае — большего), поэтому объем крайнего термина, который входит в объем среднего, исключается из объема другого крайнего термина (схема 35).

2-е правило: хотя бы одна из посылок должна быть общим суждением.

Из правила следует:

а) Из двух частных посылок заключение с необходимостью не следует.

Если обе посылки — частноугвердительные суждения ( II), то вывод сделать нельзя согласно 2-му правилу терминов: в частноутвердительном суждении ни субъект, ни предикат не распределены, поэтому и средний термин не распределен ни в одной из посылок.

Если обе посылки — частноотрицательные суждения ( ОО), то вывод сделать нельзя согласно 1-му правилу посылок.

Если одна посылка — частноугвердительная, а другая — частноотрицательная ( IOили OI), то в таком силлогизме распределенным будет только один термин — предикат частноотрицательного суждения (1). Если этим термином будет средний, то вывода сделать нельзя, так, согласно 2-му правилу посылок, заключение должно быть отрицательным. Но в этом случае предикат заключения должен быть распределен, что противоречит 3-му правилу терминов: больший термин, не распределенный в посылке, окажется распределенным в заключении; если же больший термин распределен (2), то вывода не следует согласно 2-му правилу терминов.

1) Некоторые М(—) есть Р(-).

Некоторые S(-) не есть М(+).

2) Некоторые М(-) не есть Р(+).

Некоторые S(-) есть М(-).

Ни один из этих случаев не дает необходимых заключений, в чем легко убедиться, подобрав соответствующие примеры.

б) Если одна из посылок — частное суждение, то и заключение должно быть частным.

Если одна посылка общеугвердительная, а другая — частноутвердительная ( AI, IA), то в них распределен только один термин — субъект общеугвердительного суждения.

Согласно 2-му правилу терминов, это должен быть средний термин. Но в таком случае два крайних термина, в том числе меньший, не будут распределены. Поэтому в соответствии с 3-м правилом терминов меньший термин не будет распределен в заключении, которое будет частным суждением. Например:

Все студенты нашего института ( М+) изучают логику ( Р—).

Некоторые сотрудники милиции ( S—) — студенты нашего института ( М—).

_________________________

Некоторые сотрудники милиции ( S—) изучают логику ( Р—).

Если одна из посылок утвердительная, а другая — отрицательная, причем одна из них частная ( EI, АО, ОА), то распределенными окажутся два термина: субъект и предикат общеотрицательного суждения ( EI) или субъект общего и предикат частного суждения ( АО, ОА). Но в том и другом случае, согласно 2-му правилу посылок, заключение будет отрицательным, т. е. суждением с распределенным предикатом. Атак как вторым распределенным термином должен быть средний (2-е правило терминов), то меньший термин в заключении окажется нераспределенным, т. е. заключение будет частным. Например:

Все врачи ( Р+) имеют медицинское образование ( М—).

Некоторые из присутствующих ( S—) не имеют медицинского образования ( М+).

_____________________

Некоторые из присутствующих ( S—) не врачи ( Р+).

1. Назовите правила терминов и посылок простого категорического силлогизма.

2. К каким логическим ошибкам ведет нарушение правил?

В посылках простого категорического силлогизма средний термин может занимать место субъекта или предиката. В зависимости от этого различают четыре разновидности силлогизма, которые называют фигурами (схема 36).

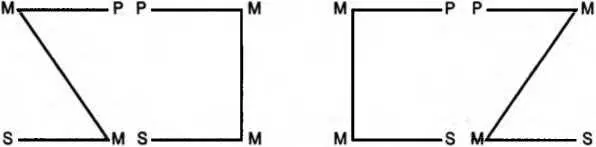
Схема 36

В первой фигуресредний термин занимает место субъекта в большей и место предиката в меньшей посылках.

Во второй фигуре— место предиката в обеих посылках.

В третьей фигуре— место субъекта в обеих посылках.

В четвертой фигуре— место предиката в большей и место субъекта в меньшей посылках.

Эти фигуры исчерпывают все возможные комбинации терминов.

Фигуры силлогизма — это его разновидности, различающиеся положением среднего термина в посылках.

Каждая фигура имеет свои особые правила, которые выводятся из общих.

Правила 1-й фигуры:

1. Бóльшая посылка — общее суждение.

2. Меньшая посылка — утвердительное суждение.

Докажем сначала 2-е правило. Если меньшая посылка будет отрицательным суждением, то согласно 2-му правилу посылок заключение также будет отрицательным, в котором Рраспределен. Но тогда он будет распределен и в большей посылке, которая также должна быть отрицательным суждением (в утвердительном суждении Рне распределен), а это противоречит 1-му правилу посылок. Если же большая посылка будет утвердительным суждением, то Рбудет не распределен.