Вадим Розин - Семиотические исследования

Например, геометрия, точнее практика, в которой использовались алгоритмы вычисления площадей полей правильной формы, а также их планы и расчеты элементов, была изобретена, когда нужно было восстанавливать границы полей, смываемых каждый год Нилом и Евфратом (см.: 14; 15; 44). И как еще, как ни катастрофу, мог древний египтянин или шумер понимать такой разлив: вода унесла межевые камни, какой теперь брать налог – неизвестно, а если налог не будет вовремя получен, боги разгневаются и отвернутся от человека, да и сама жизнь будет под угрозой. Но рассмотрим подробнее, как, например, сложился алгоритм вычисления прямоугольного поля.

Так как разливы рек смывали границы полей, перед древними народами каждый год вставала задача – восстанавливать границы, при этом необходимо было, чтобы каждый земледелец получил ровно столько земли, сколько он имел до разлива реки. Судя по археологическим данным и сохранившимся названиям мер площади, данная проблема частично была разрешена, когда размер каждого поля стали фиксировать не только границами, но и тем количеством зерна, которое шло на засев поля. Действительно, наиболее древняя мера площади у всех древних народов – «зерно» – совпадает с мерой веса, имеющей то же название.

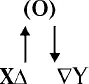
(схема 8)

Здесь Х – поле, подлежащее восстановлению, Y – восстановленное поле примерно той же величины, М – количество мер зерна, идущее на восстановление поля.

Однако восстановление полей с помощью зерна не всегда было возможным или удобным: часто необходимо было восстановить поле, не засеивая его, засеивать можно было по-разному, получив больше или меньше площади, и т. д. Эмпирический материал подсказывает, что был изобретен новый способ восстановления полей: теперь для восстановления прямоугольного поля Y, равного по величине полю Х, подсчитывали количество оставленных плугом в поле гряд С (их толщина была стандартной), а также длину одной их гряд С'. В языке древних народов «гряда» – это не только название части поля, но и мера площади.

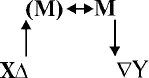
(схема 9)

Введение эталонной гряды, подсчет количества гряд и их длины тоже не разрешали всех затруднений, поскольку в древнем земледелии постоянно приходилось решать задачи на сравнение по величине двух и более полей. Предположим, имеются два поля, которые надо сравнить. В первом поле 25 гряд и каждая гряда имеет протяженность 30 шагов, а в другом – 50 гряд протяженностью в 20 шагов. Спрашивается, какое поле больше и на сколько? Сделать это, сравнивая числа, невозможно: у первого поля бо́льшая протяженность гряды, но, с другой стороны, меньше гряд. Однако поля можно сравнить по величине, если у них или одинаковое количество гряд или одинаковая протяженность (длина) гряды. Именно к этой ситуации старались прийти древние писцы и землемеры. Заметив, сравнивая урожаи полей, что величина поля не изменится, если длину гряды (количество гряд) увеличить в n раз, и соответственно количество гряд (длину гряды) уменьшить в n раз, они стали преобразовывать поля, но не реально, а в плоскости замещающих их знаков (чисел). Например, чтобы решить приведенную здесь задачу, нужно количество гряд в первом поле увеличить в два раза (25×2=50), а длину гряды, соответственно, уменьшить в два раза (30:2=15). Так как в Древнем мире обычно сравнивали большое количество полей разной величины (например, в Древнем Вавилоне сразу сравнивали несколько сотен полей), то постепенно сложилась практика приведения длины гряды к самой маленькой длине полей и, в конце концов, к единице длины (один шаг, локоть). Соответственно, чтобы не изменилась величина поля, количество гряд умножали на длину полей. Например, для полей, величина которых выражается числами – 10,40, 5,25, 15,20, 2,30, получалась следующая таблица:

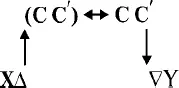
или после соответствующих арифметических операций:

Поскольку слева всегда получается число 1, то величина поля выражается только числами и операциями в правом столбце, т. е. произведением длины гряды на количество гряд . Естественно предположить, что этот факт рано или поздно был осознан древними писцами, они стали опускать числа 1 левого столбца и построили принципиально новый способ вычислений: сначала измеряли количество гряд и длину средней гряды (у прямоугольного поля – это любая гряда, у трапециидального и треугольного – среднее арифметическое самой большой и самой маленькой длины), а затем вычисляли величину поля, перемножив полученные числа (14; 15; 44). Но если бы, например, шумерскому писцу, впервые нашедшему формулу вычисления площади прямого поля, сказали, что он что-то там сочинил или придумал, он бы все это отверг как кощунство и неверие в богов. Выводя данную формулу, он считал, что всего лишь описывает, как нечто было устроено богом, что сам бог в обмен на его усердие и богопочитание открывает ему знание этого устройства.

Рассмотренный здесь этап как действия со знаками можно записать так:

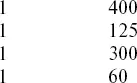
(схема 10)

Здесь ♠ – описанные выше операции преобразования с числами, вплоть до конечной – умножения числа С на С'.

Второй пример относится к реконструкции способов решения шумеро-вавилонских задач.

Реконструируя способы решения вавилонских задач, историки математики оказываются перед лицом парадоксов. С их точки зрения, шумеро-вавилонские математики решали задачи, которые сегодня проходят по ведомству алгебры, геометрии или теоретической арифметики, именно на основе соответствующих математических дисциплин, в то время как последние сложились спустя два-три тысячелетия. Этот парадокс не случаен. Дело в том, что речь в данном случае идет не столько о математике, сколько о математическом мышлении, а мышление, как известно, изучается прежде всего в логике, психологии, теории культуры. Наделяя вавилонских математиков современным стилем и характером мышления, историки математики нарушают, к примеру, некоторые основные принципы исторического рассмотрения культур, принципы исторического анализа человеческого сознания, мышления и поведения. Согласно этим принципам, шумеро-вавилонская культура самобытна и не похожа на современную, языки, сложившиеся в этой культуре (и математические в том числе), принципиально отличны от современных, мышление и поведение представителей шумеро-вавилонской культуры своеобразны и определяются всем строем данной культуры и ее историей.