Михаил Попов - Собрание сочинений. Том 1

Возможные варианты развития объективны, интересы рабочего класса — объективны. Объективно, следовательно, и предпочтение на множестве вариантов развития, указывающее, какой вариант, с точки зрения интересов рабочего класса, лучше, какой хуже. Объективно существует, следовательно, вариант или множество эквивалентных друг другу вариантов, которые лучше всех других удовлетворяют интересам рабочего класса. Иными словами, существует элемент или множество элементов из множества 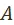, оптимальных с точки зрения предпочтения .

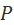Сказанное может натолкнуть на мысль, что задача оптимизации социалистической экономики состоит в нахождении множества элементов из 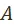, оптимальных с точки зрения предпочтения 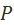. Однако этот вывод был бы преждевременным. Ни плановые органы, ни экономическая наука в действительности никогда не познают до конца, во всей полноте ни множества 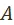, ни предпочтения 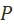. Всегда придётся довольствоваться лишь относительной истиной. Поэтому в действительности вместо одной идеальной задачи оптимизации мы имеем три реальные.

1. Задача определения множества вариантов развития: получать все более полное и более точное представление 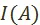о множестве объективно возможных вариантов развития социалистической экономики 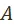. Элементы множества 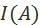— познанные, плановые варианты развития.

2. Задача познания предпочтения, объективно заданного на множестве объективно возможных вариантов развития 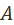: полнее и глубже познавать исторические интересы рабочего класса, интересы общественного развития. Достигнутая ступень в этом познании может быть записана как предпочтение 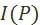, заданное на некотором подмножестве множества 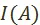. Мы обращаем внимание на то, что 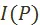задаётся, вообще говоря, не на всем множестве 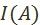. Этим подчёркивается тот факт, что не обязательно относительно любых двух известных плановых вариантов можно на данном этапе развития экономической науки сказать, какой в большей, а какой в меньшей степени соответствует интересам общественного развития, интересам рабочего класса.

3. Собственно задача оптимизации: найти элемент или множество элементов из множества 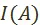, оптимальные с точки зрения предпочтения 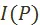. Другими словами: выбрать из всех имеющихся налицо плановых вариантов развития социалистической экономики наилучший с точки зрения интересов рабочего класса.

Заметим, что было бы очень удобно, если бы удалось построить функцию на 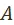, соответствующую предпочтению 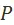на этом множестве, обладающую следующими свойствами. Вариант 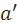предпочтительнее варианта 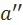в смысле предпочтения 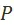, в символической записи 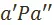тогда и только тогда, когда 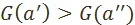, вариант 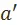эквивалентен варианту 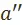в смысле предпочтения 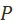, , 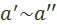тогда и только тогда, когда 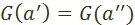. Однако такое представление совсем не обязательно существует (существование здесь, разумеется, понимается в математическом смысле), это во–первых. А во–вторых, если оно и существует, то остаётся лишь удобным для дальнейших исследований сокращением, но ни на шаг не продвигает нас в познании самого предпочтения. Если я не знаю предпочтения, то я не могу построить и функции, изображающей это предпочтение, представляющей его.

Вернёмся, однако, к нашей реальной задаче оптимизации. Поскольку мы интересуемся только проблемой выбора вариантов, то можем оставить в стороне процесс нахождения множества 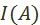. Здесь мы предполагаем, что множество плановых вариантов 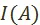нам дано. Обращаем внимание на то, что множество 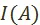не является подмножеством множества 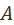. Если элемент множества 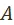— объективно возможный вариант развития, взятый во всей полноте, во всем богатстве его составляющих, то элемент множества 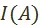не даёт всей картины развития и, конкретизируя начальный этап развития, оставляет неясными очертания будущего.

Поскольку решения первой из перечисленных выше задач мы здесь не касаемся, перед нами остаются, во–первых, задача нахождения предпочтения 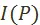и, во–вторых, задача выбора оптимального в смысле этого предпочтения решения из множества плановых вариантов 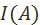. Эти две задачи весьма тесно связаны между собой, но чисто экономической задачей является лишь задача нахождения 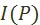. После её решения задача нахождения оптимального плана развития становится математической задачей выбора из множества плановых вариантов оптимального с точки зрения заданного предпочтения.

Точно так же, как для множества 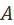и предпочтения 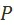, для множества 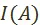и предпочтения 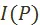, быть может, существует порядковая функция g, описывающая это предпочтение. И так же, как и в предыдущем случае, без знания предпочтения 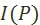функция 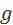остаётся лишь краткой записью нашей неосведомлённости о предпочтении; «целевая» функция, поставленная в задаче оптимизации, является тогда лишь записью того, что мы абстрагируемся от выяснения предпочтения и предполагаем его данным.