Михаил Попов - Собрание сочинений. Том 1

Summary

This paper is devoted to defining conditions under which the rate of growth of means of production in the Lenin’s model is greater than the rate of growth of consumer production.

The conditions are derived also for the case when only a part of the- value of the constant capital is carried on the product during one period of production.

Статья поступила в редакцию 15 октября 1969 г.

Настоящее сообщение ставит своей целью на одном примере продемонстрировать возможность использования математики для решения теоретических проблем политической экономии.

Положение о том, что цены производства на продукцию I подразделения стоят выше стоимости, а на продукцию II подразделения — ниже, и, следовательно, что цены производства перераспределяют стоимость из II подразделения в I, было строго доказано Марксом в «Капитале» лишь для того случая, когда применяемый капитал совпадает с потребляемым и исчислен в стоимости, а не в ценах производства. В действительности же применяемый капитал чаще всего больше потребляемого и исчислен уже через цены производства, причём именно по отношению к исчисленной таким образом величине применяемого капитала справедливо положение: цены производства приносят равную прибыль на равный капитал.

Однако учёт этого реального факта потребовал бы, как кажется, знания тех цен производства, которые ещё только должны быть выведены из условия: равная прибыль на равный капитал. Мы попадаем, следовательно, в «заколдованный круг», выйти из которого без использования математики было бы весьма затруднительно. Математическим же путём доказать упомянутое выше Марксово положение нетрудно, приняв во внимание как тот реальный факт, что составляющие капитал факторы приобретались уже по ценам производства, а не по стоимости, так и тот, что потребляемый капитал не тождествен с применяемым и составляет только часть последнего.

Перейдём к доказательству.

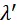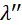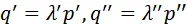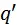Обозначим через и множители, показывающие, во сколько раз цена производства соответственно средств производства и предметов потребления больше их стоимости, т. е. , где и 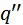– цены производства средств производства и предметов потребления, а 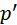и 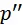– их стоимости.

Для того чтобы доказать, что цены производства на продукцию I подразделения стоят выше стоимости, а на продукцию II подразделения — ниже, достаточно доказать, что .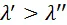

В самом деле, невозможно, чтобы 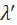и 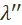были бы одновременно больше или одновременно меньше единицы. Это означало бы тогда (в силу равенства суммы цен производства сумме стоимостей 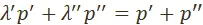) либо, что , либо, что 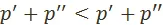. Значит, один из 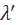и 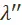меньше единицы, а другой больше. Если доказать, что 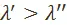, то в силу того, что один из них меньше единицы, а другой больше, будем иметь: 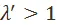, а 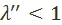. 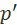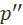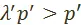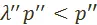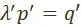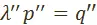Помножив первое неравенство на , а второе на , получим , а , или, приняв во внимание, что , а , получим: 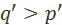, a 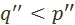. Последние два неравенства и есть запись доказываемого положения: цены производства на продукцию I подразделения стоят выше стоимости, а на продукцию II подразделения — ниже.

Следовательно, если мы докажем, что 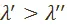, то доказательство будет закончено. Приступим к доказательству этого неравенства.

Возьмём величину 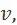не превосходящую ни величины переменного капитала I подразделения, ни величины переменного капитала II подразделения, и выделим мысленно из подразделений части с переменным капиталом одинаковой величины 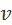. Эти части всегда можно взять такими, что отношения цен производства и стоимости продукции в них будут равны отношениям цен производства и стоимости всей продукции соответствующих подразделений. В качестве таких частей можно выделить, например, части, являющиеся по объёму и номенклатуре продукции лишь пропорционально уменьшёнными копиями подразделений. В силу различного строения капиталов I и II подразделений и равенства переменных капиталов выделенных частей соответствующие этим частям постоянные капиталы связаны неравенством .

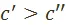Предполагаем одинаковой норму прибавочной стоимости в обоих подразделениях. Тогда равным переменным капиталам 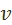будут отвечать одинаковые по величине прибавочные стоимости 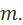Стоимость продукции, соответствующей первому из выделенных капиталов, равна 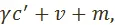а стоимость продукции, соответствующей второму капиталу, 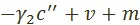, где 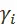– доля потреблённого капитала в применяемом,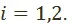

Цены производства продукции, соответствующей выделенным капиталам, равны соответственно 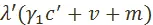и 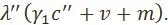Мы воспользовались здесь тем, что коэффициенты 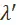и 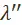связывают между собой стоимости и цены производства. Но цена производства продукции может быть выражена как издержки производства плюс средняя прибыль. Учтя это и обозначив общую норму прибыли через 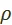, получим следующие 2 равенства: