Carlos Casado - Вначале была аксиома. Гильберт. Основания математики

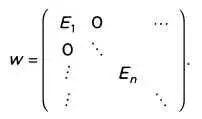
Посмотрим, как квантовые механики решали проблему нахождения различных энергетических уровней электрона атома водорода. В матричной механике нужно было «диагонализовать» матрицу Гамильтона Н, измеряющую общую энергию системы, то есть определить матрицу S так, чтобы матрица W = S -1HS была диагональной; так диагональные элементы Е n— это энергетические значения электрона:

В свою очередь, в волновой механике требовалось решить волновое уравнение Шрёдингера, то есть следующее уравнение в частных производных:

-Δψ + Vψ = Εψ,

где ψ — волновая функция (независимая от времени), V — потенциал, а Е — энергия. Если определить оператор Гамильтона как Η = -Δ + V (то есть кинетическая энергия плюс потенциальная энергия), предыдущее уравнение можно переписать, чтобы оно приняло вид Ηψ = Εψ и представляло собой то, что известно как проблема собственных значений, или проблема Штурма — Лиувилля, поскольку ею занимались французские математики Жак Шарль Франсуа Штурм (1803-1855) и Жозеф Лиувилль (1809-1882). Она называется так, поскольку это последнее уравнение допускает решение для некоторых значений ψ и Е, которые получают название собственных функций и собственных значений, соответственно.

В классической физике собственные значения определяли, например, характерные частоты колебания упругой мембраны, так что любое колебание могло выражаться как наложение этих базовых видов колебания. В квантовой физике собственные значения Е п— это как раз возможные уровни энергии электрона атома водорода. Разницы между этими собственными значениями дают частоты испускаемых квантов света (фотонов), описывая таким образом структуру спектра излучения атома. В свою очередь, различные состояния электрона заданы собственными функциями ψn, соотносящимися с собственными значениями. В математике множество собственных значений Еn матрицы или оператора называется спектром. В результате чудесного совпадения математический спектр (название для которого Гильберт выбрал случайно) в итоге стал ключевым для объяснения физических спектров атомов. Ученый говорил: «Я разработал теорию о бесконечных переменных и даже назвал ее спектральным анализом, совсем не предполагая, что позже она найдет применение для настоящего физического спектра». Это была счастливая случайность.

Жак Шарль Франсуа Штурм

Жозеф Лиувилль.

Кроме того, он выяснил, что эти множества чисел (соответствующие коэффициентам Фурье классического выражения движения электрона) не коммутируют. Другими словами, в отличие от классических величин, квантовые в целом выполняют QP ≠ PQ. Через несколько месяцев двое коллег из Геттингена, физик Макс Борн и математик Паскуаль Йордан (1902-1980), признали, что эти множества чисел Q и Р ведут себя как математические матрицы (хотя сам Гейзенберг, по его словам, даже не знал, что такое матрица). Матричная квантовая механика выросла в саду, возделанном Гильбертом. Однако Геттинген разделился на две группы: Гильберт и его сторонники верили в большой успех, обусловленный введением матричного исчисления в физику, а их противники отмахивались от утомительной метаматематики, наполнившей атомную физику.

В рождественские каникулы 1925-1926 года Эрвин Шрё- дингер (1887-1961) осветил волновую квантовую механику, пока наслаждался обществом своей последней возлюбленной (по словам Германа Вейля, его коллеги по Цюриху). В отличие от юных физиков и математиков Геттингена, но как представителю значительной части старой гвардии, Шрёдингеру не очень импонировала квантовая механика Гейзенберга, Борна и Йордана. В поисках интуитивно более понятной теории, в которой бы применялись только классические математические инструменты, он вывел свое знаменитое волновое уравнение. Идея возникла при изучении движения электрона, как если бы речь шла о волновом движении, волновая функция Ψ которого отвечала бы за описание состояния системы. Его работа была принята с воодушевлением, потому что решить дифференциальное уравнение — чем физики занимались уже несколько веков — казалось намного проще, чем найти решение некоторых матричных уравнений.

Итак, панорама, которая была представлена физикам в начале весны 1926 года, не могла быть более парадоксальной: в их распоряжении имелись две механики, которые объясняли и прогнозировали одни и те же явления, несмотря на то что в каждой использовался абсолютно разный подход и намечалась абсолютно разная концепция микрокосмоса. Если Шрёдингер называл матричную механику «противоестественной», то Гейзенберг не сдавался и окрестил волновую механику «отталкивающей». Некоторые физики — сам Шрёдингер, Карл Эккарт (1902-1973) и Вольфганг Паули (1900-1958) — стремились прояснить формальные отношения между обеими механиками. Они пришли к выводу, что оба механизма математически эквивалентны, хотя их доказательство того, что можно построить матрицы Q и Р на основе волновых функций Ψ и наоборот, было не совсем корректным.

В признании сходства между двумя механизмами есть заслуга Гильберта. Он посмеивался над Борном и Гейзенбергом, так как, открыв матричную механику, они столкнулись с теми же трудностями, с которыми, конечно же, сталкиваются все математики, работающие с бесконечными матрицами. Когда они обратились за помощью к Гильберту, он сказал им (вспомнив свою работу над интегральными уравнениями 20-летней давности), что единственный раз он столкнулся с матрицами, когда те появлялись как побочный продукт изучения собственных значений дифференциального уравнения с граничными условиями (то есть когда интегральное уравнение преобразовывалось в систему бесконечных линейных уравнений). Он предположил, что если они найдут дифференциальное уравнение, порождающее эти матрицы, то, возможно, получат больше информации. Гейзенберг и Борн подумали, что он сказал это для того, чтобы отвязаться от них, а на самом деле не знал решения этого вопроса. Позже Гильберт шутил, указывая на то, что если бы они его тогда послушали, то открыли бы волновую механику Шрёдингера на полгода раньше него. Это был путь, по которому шли Шрёдингер, Эккарт и Паули, чтобы показать идентичность обеих теорий с математической точки зрения.