Carlos Casado - Вначале была аксиома. Гильберт. Основания математики

Единственная цель теоретической физики состоит в вычислении результатов, которые могут быть сравнены с опытом, и вовсе нет необходимости в утвердительном описании всего хода явлений.

Поль Дирак

Осенью 1926 года Паскуаль Йордан и британский физик Поль Адриен Морис Дирак (1902-1984) независимо друг от друга начали разрабатывать теорию преобразований, чтобы раз и навсегда объединить квантовые механики. Так как квантовые величины, введенные Гейзенбергом, определяли новый тип алгебры (для него умножение не было коммутативным), Дирак решил назвать q-числами величины, которые так себя ведут (хотя q здесь происходило не от слова quantum, а от английского queer, то есть «странный», «необычный»). Итак, абстрактная алгебра #-чисел допускает различные представления или образы (так же как одна и та же система аксиом может допускать разные модели), два из которых — матричная и волновая механика.

В матричной механике речь шла о поиске матрицы S, чтобы матрица W = S -1HS была диагональной. Если выделить HS в этом уравнении, получается HS = SW. И если, применяя правило умножения матриц, записать то, что означает это последнее уравнение для элементов каждой матрицы, можно получить систему бесконечных линейных уравнений (напоминает получившуюся при преобразовании интегрального уравнения):

∞

∑h pqS qn= E nS pn. [1]

q=1

С другой стороны, в волновой механике пытались решить волновое уравнение Шрёдингера Ηψ = Εψ, определяя собственные значения, являющиеся решением. Если в уравнение ввести собственную функцию ψ n, назначенную собственному значению Е n, получается:

Ηψ n= Ε nψ n. [2]

Как Гильберт, так и Дирак, переформулировав обе проблемы в таком виде, перешли к их сравнению и заметили, что [1] и [2] представляют собой схожую структуру: Гамильтониан x ΧΥΖ = Энергия x ΧΥΖ. Следовательно, вопрос, которым они задались, звучал так: какие условия следует допустить, чтобы приравнять член к члену уравнения [1] матричной механики к уравнению [2] волновой механики? Так как «интегрирование» в царстве непрерывного — это аналог «сложения» в царстве дискретного (символ ∫ происходит от последовательной деформации прописной S), они решили: то, что должно заменить (при переходе от дискретного к непрерывному) первый член в [1], будет выглядеть как ∫h(х,у)ψ n(у)d(у). Значит, объединение между обеими квантовыми механиками было бы достигнуто, если бы последнее выражение совпадало с первым членом в [2] в виде:

Ηψ n(x) =∫h(x,у)ψ n(у)dy,

то есть если бы любой оператор Гамильтона мог быть записан как интегральный оператор.

Но это было невозможно даже для такого простого оператора, как тождество (определяемое как Ηψ = ψ для любой волновой функции). Дирак не спасовал перед трудностями и, чтобы преодолеть их, прибегнул к функции δ. Эта своеобразная функция определена δ(z)=0 для любого z≠0[3] и, как ни парадоксально, ∫δ(z)dz= 1 [4]. Как представить себе функцию, которая равна 0 во всех точках, кроме одной, и интегрирует 1?

Итак, приняв эту функцию и рассматривая h(x,y)=δ(x-y) как ядро вышеприведенного интегрального уравнения, можно выразить тождество, например, как интегральный оператор, просто применив магические свойства δ:

[3] [4]

Ηψ(x)=∫h(х,у)ψ(у)dy=∫δ(х-у)ψ(у)dy= ψ(x)∫δ(x-y)dy=ψ(x)·1=ψ(x).

С помощью подобных вычислений можно доказать, что любой оператор может быть представлен как интегральный оператор, так что обе квантовые механики оказываются принудительно унифицированными.

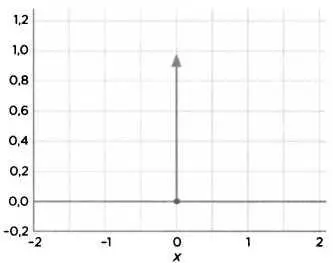
Схематическая диаграмма дельты Дирака: «функция», которая равна 0 во всех своих точках, кроме начала, где она равна бесконечности, чтобы таким образом интегрировать 1.

Для того чтобы все преобразования между представлениями квантовой механики работали корректно, Дирак был вынужден прибегнуть к использованию вымышленной математической сущности — дельта-функции, которая на самом деле функцией не была. Для физиков это стало полезной идеализацией, привести которую к строгому виду должны были математики. Для математиков, наоборот, это понятие оказалось подозрительным и не обладающим математической реальностью, его использование оправдывалось только физическими применениями. Дельта-функцию Дирака ждала печальная участь, поскольку лишь в 1950 году она нашла свое место в рамках теории распределений, созданной Лораном Шварцем (1915-2002). До этого из-за отсутствия у нее строгости она оставляла равнодушными математиков Гёттингена.

И именно тогда в Гёттинген приехал молодой Джон фон Нейман, чтобы поработать в качестве помощника Гильберта. Блестяще защитив докторскую диссертацию по теории множеств, он начал читать лекции по функциональному анализу вместе с Эрхардом Шмидтом в Берлине. В то время Гильберт пытался найти рациональную математическую модель для квантовой механики; но его аксиоматический подход развивался медленно, потому что ученый страдал злокачественной анемией (смертельным заболеванием, от которого он исцелился благодаря нетрадиционным методам). В 1926-1927 году Гильберт попросил своего ассистента по физике Лотара Нордгейма разложить для него по полочкам суть последних исследований, чтобы иметь возможность читать курс квантовой механики, применяя свой любимый аксиоматический метод. Фон Нейман вдохнул жизнь в проект. Под предводительством Гильберта они втроем ринулись искать строгое математическое оформление. Так, в 1927 году они вместе написали статью «Об основаниях квантовой механики». Гильберт хотел заставить работать интегральную формулировку физических проблем, более практичную, чем дифференциальный вариант, выраженный посредством волнового уравнения или дискретной версии в матричных терминах. Так же как и венгерский физик Корнелий Ланцош (1893-1974) в 1926 году (что любопытно, за месяц до того, как Шрёдингер опубликовал свое знаменитое уравнение), Гильберт, Нордгейм и фон Нейман разработали квантовую механику, пользуясь интегральными уравнениями. Однако результат этого первого приближения не был удовлетворительным, поскольку они не смогли избежать тупика дельты Дирака, чтобы перейти от одной формулировки к другой.

Фон Нейман закончил работу по аксиоматическому обоснованию квантовой механики в одиночку. Он сделал это в период с 1928 по 1932 год, опубликовав серию из пяти статей и монументальный трактат «Математические обоснования квантовой механики». Чтобы придать прочную математическую основу квантовой теории, он отказался от использования дельта-функций Дирака и от предпочтения интегральных уравнений Гильберта. У него было другое оружие: функциональный анализ. Он создал абстрактное аксиоматическое обрамление, гильбертово пространство, которое включало в себя частные матричный и волновой случаи.