Juan Carretero - Темная сторона материи. Дирак. Антивещество

E = √(c 2р 2+ m 2с 4) (свободная частица).

Самосопряженные операторы (эрмитовы операторы) важны для квантовой теории, поскольку присущее им собственное значение является действительным. В случае оператора Гамильтона «самосопряженность» гарантирует нам, что энергия системы, которую мы изучаем, будет действительной. Оператор называют самосопряженным, когда он совпадает со своим сопряженным. Возьмем общий случай квантового оператора, представленного в матричной форме матрицы 2x2:

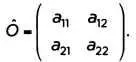
Сопряженный оператор задан матрицей, выстроенной из изначальной матрицы, в которой изменяются строки и столбцы, и каждый элемент заменен комплексно-сопряженным ему элементом. Такая матрица называется сопряженной:

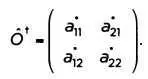
Если две матрицы согласуются друг с другом, то есть если Ó = Ö, говорят, что матрица Ó является эрмитово-сопряженной, и в этом случае можно доказать, что ее значения являются действительными. Три матрицы Паули, σ x,σ y,σ z, являются эрмитово-сопряженными, и они «антикоммутативны» между собой, то есть соблюдают общие отношения, вытекающие из уравнения Дирака. Однако можно доказать, что любая матрица размера 2x2 может быть записана в виде линейной комбинации трех матриц Паули плюс единичная матрица. Это означает, что невозможно найти четвертую матрицу, которая антикоммутативна каждой из трех матриц Паули. Иными словами, уравнение Дирака требует, чтобы размер каждого из четырех матричных коэффициентов, подлежащих определению, был больше 2x2. Кроме того, матрицы Дирака удовлетворяют антикоммутационным соотношениям, и их след равен нулю.

В итоге его требования к новому квантовому релятивистскому уравнению электрона можно описать следующим образом.

1. Это должно быть дифференциальное уравнение первого порядка по времени, которое симметрично включает пространственные переменные, то есть с производными первого порядка.

2. Оператор Гамильтона должен быть самосопряженным — так, чтобы плотность вероятности определялась положительным значением и чтобы энергии были действительными.

3. Оно должно согласовываться с релятивистским выражением для энергии и быть релевантным для любой инерциальной системы отсчета.

Таким образом, Дирак предложил следующее общее уравнение:

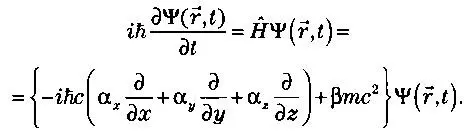
Заметим, что два вида переменных — пространство и время — включены одним способом. Кроме того, существует дополнительный член уравнения, ßmc 2, связанный с собственной массой электрона, то есть с массой в системе, в которой он находится в состоянии покоя. Уравнение зависит от четырех неизвестных коэффициентов: α x,α y,α z,β. Таким образом, вопрос состоит в том, как их определить. Для этого Дирак должен был доказать совместимость своего уравнения с релятивистским выражением для энергии.

Он полностью осознавал «эквивалентность» квантовых операторов и соответствующих классических величин. Кстати, именно это соответствие позволило объяснить форму уравнения Шрёдингера и уравнения Клейна — Гордона. Используя аналогию между классическим и квантовым миром, квантовое уравнение, предложенное Дираком, вело к следующему классическому уравнению для энергии:

Е= с (α xp x+ α yр y+ α zp z) + ßmc 2.

Как связать данное уравнение, линейное в трех составляющих кинетического момента со сложным релятивистским выражением энергии, в котором появляется квадратный корень? Дирак искал способ, позволивший бы ему записать в линейном виде релятивистское уравнение энергии, определив четыре неизвестных коэффициента. Первым большим шагом вперед в этом направлении было открытие того, что его квантовое уравнение может быть совместимым с релятивистским выражением для энергии, только когда введенные им коэффициенты не коммутируют между собой и, кроме того, если квадрат каждого оператора равен единице. Математически это выражается в следующей форме:

α i α j= - α jα i(i ≠ j); α iβ = - βα i;α i= β 2= 1.

Индексы i,j относятся к любой из трех пространственных составляющих: х, у, z. Коэффициенты Дирак интерпретировал как матрицы. Последнее означало, что волновая функция Ψ содержит разные составляющие, помимо своей зависимости от временных и пространственных переменных. Это было новостью. В предыдущем 1927 году Паули уже представил волновую функцию с двумя составляющими, связанными с двумя возможными значениями спина.

Однако проблема была решена не до конца. Сопряженность гамильтониана означала, что четыре матрицы должны быть, в свою очередь, эрмитово-сопряженными. В первое время Дирак думал о матрицах Паули, которые отвечали всем необходимым условиям. Но матриц Паули было три, и Дираку надо было найти четвертую, чтобы окончательно сформировать уравнение. В результате он пришел к выводу, что найти четвертую матрицу для трех матриц Паули невозможно. Математики на самом деле уже знали этот результат, так как они доказали, что для квадратных матриц Nx N максимальное количество независимых эрмитово-сопряженных матриц, которые «антикоммутируют» между собой, равно N 2-1. Следовательно, у Дирака оставалась единственная возможность — увеличить размер матриц. Доказав, что их размер обязательно должен быть парным, ученый наконец нашел четыре независимые эрмитово-сопряженные матрицы 4x4. Это минимальный размер, который согласуется с общими свойствами его уравнения. Дирак заметил:

«Мне понадобилось много недель, чтобы осознать, что необязательно использовать переменные с двумя строками и двумя столбцами. Почему бы не представить четыре строки и четыре столбца?»

Уравнение Дирака запечатлено на его мемориальной доске в Вестминстерском аббатстве. На самом делетам оно присутствует в своей «ковариантной форме». Это значит, что форма уравнения является одинаковой для любой инерциальной системы отсчета. Для упрощения записи уравнения в квантовой релятивистской теории принято одновременно считать редуцированную постоянную Планка, h, и скорость света, с, равными единице. Это называется «естественной системой единиц». В таком случае уравнение Дирака записывается так:

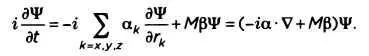
В него включен оператор Гамильтона,