Алекс Беллос - Алекс в стране чисел. Необычайное путешествие в волшебный мир математики
- Название:Алекс в стране чисел. Необычайное путешествие в волшебный мир математики
- Автор:
- Жанр:
- Издательство:КоЛибри
- Год:2012
- Город:Москва
- ISBN:978-5-389-01770-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Алекс Беллос - Алекс в стране чисел. Необычайное путешествие в волшебный мир математики краткое содержание
Алекс Беллос, известный журналист, многие годы работавший для «Guardian», написал замечательную книгу о математике. Книга эта для всех — и для тех, кто любит математику, и для тех, кто считает ее невероятно скучной и далекой от жизни. Беллосу удалось создать настоящий интеллектуальный коктейль, где есть и история, и философия, и религия, и конечно же математика — чудесные задачки, которые пока не решишь, не заснешь!
Алекс в стране чисел. Необычайное путешествие в волшебный мир математики - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Сравним приведенное вычисление с умножением столбиком, которое все мы изучали:
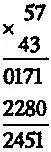
Имеется очень простая причина, по которой наш метод и проще, и быстрее. Дело в том, что ни римляне, ни греки, ни евреи не изобрели символа для нуля. А когда дело доходит до вычислений, то именно 0, то есть ничто, становится невероятно важным и меняет все кардинальным образом.
Веды, священные индуистские тексты, передавались из поколения в поколение из уст в уста, пока наконец их не перевели на санскрит около двух тысяч лет назад. В одном ведическом пассаже о построении алтарей перечисляются следующие слова, обозначающие числа:
| Даса | 10 | Арбуда | 10 000 000 |
| Сата | 100 | Ньярбуда | 100 000 000 |
| Сахастра | 1000 | Самудра | 1 000 000 000 |
| Аюта | 10 000 | Мадхья | 10 000 000 000 |
| Ньюта | 100 000 | Анта | 100 000 000 000 |
| Праюта | 1 000 000 | Парардха | 1 000 000 000 000 |
При наличии названий для каждого числа, кратного десяти, удается эффективно описать большие числа, из чего астрономы и астрологи (и, надо полагать, строители алтарей) почерпнули подходящий к своим задачам лексикон для огромных величин, требуемых в их вычислениях. В этом одна из причин, по которым индийская астрономия опережала свое время. Возьмем число 422 396. Индусы начинали с самой младшей цифры — той, что справа, — и последовательно описывали число, переходя справа налево: «шесть и девять дасы и три сахастры и две аюты и две ньюты и четыре праюты». Не так уж сложно осознать, что при этом можно не указывать степени десятки, потому что значение числа в списке определяется его положением. Другими словами, приведенное выше число можно было бы записать и просто как «шесть, девять, три, два, два, четыре».
Исчисление такого типа известно как «позиционная» система, и мы рассматривали ее выше. Бусинка на абаке имеет различные значения в зависимости от того, к какому столбцу она относится. Подобным же образом каждое число в приведенном выше списке имеет значение в зависимости от своей позиции. Но при этом позиционная система требует какой-то идеи для «заполнения места» в том случае, когда в данном столбце или в данной позиции никакого числа нет. Например, если в числе имеется две дасы, ни одной саты и три сахастры, то его нельзя записать как «два, три», потому что такая запись указывает на число, в котором две дасы и три саты. Заполнитель места требуется для того, чтобы ясно сигнализировать отсутствие саты, и индусы использовали для этого слово «шунья», означавшее «пустота». Наше число поэтому есть «два, шунья, три».
Индусы были не первыми, кто ввел в обиход заполнитель места. Честь этого изобретения, судя по всему, принадлежит вавилонянам, которые записывали свои числовые символы в столбцы, применяя систему с основанием 60. Одна колонна отводилась для единиц, вторая — для «шестидесяток», следующая — для чисел, кратных 3600, и т. д. Если в числе не было значения, соответствующего заданному столбцу, то изначально там не писали ничего. Но это приводило к путанице, так что в конце концов вавилоняне ввели символ, обозначавший отсутствие значения. Правда, этот символ использовался только как элемент разметки.
Индусы же, приняв шунью за заполнитель места, на этом не остановились, а, наоборот, повысили его в ранг полноценного числа — нуля. В наши дни нет ничего сложного в том, чтобы воспринимать нуль как число. Но на самом деле эта идея далеко не очевидна. Западные цивилизации, например, так и не пришли ни к чему подобному даже за тысячи лет математических изысканий. Действительный масштаб концептуального скачка, совершенного в Индии, хорошо иллюстрируется тем фактом, что Древний мир, имея нуль перед своим носом, глядел прямо сквозь него. Абак содержал в себе концепцию нуля уже потому, что он опирался на позиционную идею. Когда римлянин желал выразить число «одна сотня и один», он передвигал бусинку в первом столбце для обозначения одной сотни, не передвигал ничего во втором столбце, что означало отсутствие десятков, и передвигал бусинку в третьем столбце, чтобы указать просто единицу. Второй, оставленный в покое столбец выражал «ничто». Вычислители на абаке знали, что к нетронутым столбцам надо относиться с тем же вниманием, что и к тем, в котором бусинки меняли положения. Но никто из них не снабдил числовым именем или символом значение, которое выражалось нетронутым столбцом.
Свои первые робкие шаги в роли полноправного числа нуль проделал под покровительством знаменитого индийского математика Брахмагупты, жившего в VII веке. Именно Брахмагупта показал, как шунья ведет себя по отношению к своим числовым братьям и сестрам. «Данное число минус шунья дает данное число», — писал он, понимая под этим, что если из положительного числа вычесть нуль, то получится то же самое положительное число: а - 0 = а. А если умножить шунью на любое число, то получится шунья — другими словами, 0 × а = 0.
Числа исходно возникли как средство счета, как абстракции, описывающие количества. Но нуль не был числом для счета в том же смысле; понимание его значения потребовало более высокого уровня абстракции. Однако чем меньше математика оказывалась привязанной к реальным вещам, тем более мощной она становилась. Обращение с нулем как с числом означало, что позиционную систему, превратившую абак в наилучший способ вычисления, прекрасно можно использовать и для записи символов. Но это не все — нуль сделал возможным появление таких понятий, как отрицательные числа и десятичные дроби, — понятий, которые мы ныне без труда постигаем в школе и которые глубоко внедрены в нашу повседневную жизнь, но ведь они вовсе не являются самоочевидными. Древние греки сумели совершить фантастические математические открытия без использования нуля, отрицательных чисел или десятичных дробей — потому что полагались на существенно пространственное понимание математики. Им представлялось бессмыслицей, что ничто может быть «чем-то». Пифагору вообразить отрицательное число было столь же трудно, как отрицательный треугольник.
Среди всех новаторских способов обращения с числами в Древней Индии самым, пожалуй, занятным был лексикон, применявшийся для описания чисел от нуля до девяти. Вместо того чтобы закрепить за каждой цифрой уникальное имя, они применяли колоритный набор синонимов. Нуль, как мы уже знаем, назывался шинья, но еще и «эфиром», «точкой», «дырой» или «змеем вечности». Единица — «землей», «луной», «путеводной звездой» или «свернувшимся молоком». Двойка выступала под названием «рука», тройка была «огнем», а четверка — «вульвой». То или иное имя выбиралось в зависимости от контекста и следовало принятым в санскрите строгим правилам версификации и просодии. Например, следующий стих представляет собой отрывок из описания манипуляций с числами в одном древнем астрологическом тексте:
Читать дальшеИнтервал:
Закладка:









