Алекс Беллос - Алекс в стране чисел. Необычайное путешествие в волшебный мир математики

Однако охотники за числом π не собирались на этом останавливаться. Все, что требовалось, дабы подобраться поближе к истинному значению этого числа, — это строить многоугольники со все большим числом сторон. Лю Хуэй, живший в Китае в III веке, применил сходный метод, используя площадь многоугольника с 3072 сторонами, и получил пять десятичных разрядов числа π : 3,14159. Два столетия спустя Цзу Чунчжи и его сын Цзу Гэнчжи продвинулись дальше еще на одну цифру, до 3,141592, что потребовало многоугольника с 12 288 сторонами.

Грекам и китайцам мешали неуклюжие обозначения. Когда в конце концов математики стали применять арабские числительные с десятичной запятой, прежние рекорды тут же пали. В 1596 году голландский учитель фехтования Лудольф ван Цейлен, используя метод удвоения, дошел до многоугольника с 60 × 2 29сторонами и нашел значение π с точностью до 20 десятичных знаков. Опус, в котором он напечатал свой результат, заканчивался так: «У кого есть охота, пусть подойдет ближе». Он продолжал вычислять и получил число π с точностью до 32 и затем 35 десятичных знаков, каковые и были высечены на его надгробии. В Германии die Ludolphsche Zahl — число Лудольфа, или лудольфово число, — до сих пор допустимо в качестве названия числа π.

В течение двух тысяч лет единственный способ определить значение числа π состоял в использовании многоугольников.

Но в XVII веке Готфрид Лейбниц и Джон Грегори открыли новую страницу в истории числа π, предложив формулу

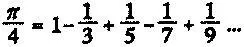
Другими словами, четвертая часть π равна единице минус одна треть плюс одна пятая минус одна седьмая плюс одна девятая и т. д.: надо попеременно прибавлять и вычитать дроби с единичным числителем и со знаменателем, последовательно равным нечетным числам, устремляющимся в бесконечность. До этого ученые видели в десятичном разложении числа π лишь случайный набор цифр. И вдруг появилось одно из наиболее изящных, ничем не усложненных уравнений во всей математике. Оказалось, что образцовый представитель беспорядка несет некий порядок в своей ДНК.

Лейбниц пришел к этой формуле, используя «анализ» — мощный раздел математики, в котором для вычисления площадей, кривых и наклонов стали применяться новые представления о бесконечно малых величинах. Формула Лейбница представляет собой так называемый бесконечный ряд — сумму, которая продолжается и продолжается без конца. И эта формула дает способ вычислить число π . Для начала нам надо умножить обе ее части на 4:

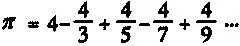
Начав с первого члена и прибавляя один за другим остальные, получаем следующую последовательность (записанную в виде десятичных дробей):

4 → 2,667 → 3,467→ 2,895 → 3,340 → …

Сумма подходит к числу π все ближе и ближе, а результат скачет все меньше и меньше. Тем не менее этот метод требует более 300 членов, чтобы ответ имел точность в два десятичных знака, так что он практически непригоден для тех, кто желает найти большее число цифр в десятичном разложении числа π.

В конце концов с помощью анализа удалось получить другие бесконечные ряды для π, менее симпатичные на вид, но более эффективные для действий с числами. В 1705 году астроном Абрахам Шарп применил такой ряд для вычисления π с точностью до 72 десятичных знаков, сокрушив продержавшийся столетие рекорд ван Цейлена, составлявший 35 знаков. Да, это было достойным достижением, но в нем было мало пользы. Решительно нет никаких практических причин для того, чтобы знать число π с точностью до 72 знаков, да, впрочем, и до 35 тоже. Инженерам, имеющим дело с прецизионными инструментами, вполне хватает четырех десятичных знаков, а чтобы вычислить длину окружности Земли с точностью до долей сантиметра, достаточно десяти знаков. Если взять 39 десятичных разрядов, то окажется возможным посчитать длину окружности, охватывающей всю известную нам Вселенную, с точностью порядка радиуса атома водорода. Дело, однако, было вовсе не в практической целесообразности — отнюдь не практические соображения двигали учеными эпохи Просвещения, одержимыми вычислением числа π. Цель охоты за цифрами заключалась в самой охоте, это было романтическое приключение. Через год после предпринятых Шарпом усилий Джон Мэчин добился точности в 100 знаков, а в 1717 году француз Тома де Ланьи прибавил к ним еще 27. К началу следующего столетия вперед вырвался Юрий Вега из Словении со своими 140 знаками.

В 1844 году, с головой погрузившись в работу на два месяца, немецкий молниеносный эстрадный вычислитель Захария Дазе отодвинул рекорд вычисления числа π до отметки 200 десятичных знаков. Дазе использовал ряд, который хотя на вид и сложнее, чем приведенная выше формула для π , но на самом деле гораздо удобнее в употреблении. Во-первых, потому что он сходится к π с неплохой скоростью. Точность в два десятичных знака достигается уже после первых девяти членов. Во-вторых, с дробями 1/ 2, 1/ 5и 1/ 8, которые все время появляются в каждом третьем члене, удобно иметь дело. Если записать 1/ 5как 1/ 10, a 1/ 8— как 1/ 2× 1/ 2× 1/ 2, то все необходимые действия с этими членами можно свести к комбинациям удвоения и взятия половины. Дазе выписал справочную таблицу, к которой обращался в ходе вычислений, начиная с 2, 4, 8, 16, 32 и далее по мере надобности. Поскольку он выполнял вычисления числа π с точностью до 200 знаков, полученное в самом конце удвоение будет иметь 200 цифр в длину. Это происходит после 667 последовательных удвоений.

Дазе использовал такое разложение:

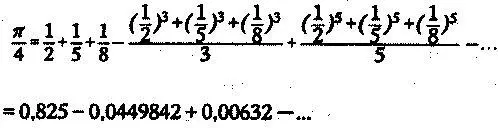
Отсюда π = 4(0,825 - 0,0449842 + 0,00632 - …).

Учет одного члена дает 3,3,

учет двух членов — 3,1200

и учет трех — 3,1452.

Дазе недолго почивал на лаврах, поскольку на его рекорд очень скоро нацелились британцы, и по прошествии десяти лет Уильям Резерфорд вычислил π с точностью в 440 знаков. Он побуждал своего протеже Уильяма Шэнкса — математика-любителя, который держал школу с пансионом в графстве Дарэм, — не останавливаться на достигнутом. В 1853 году Шэнкс достиг 607 знаков, а в 1874-м — 707. Его рекорд продержался семьдесят лет, пока Д. Ф. Фергюсон из Королевского морского колледжа в Честере не нашел ошибку в вычислениях Шэнкса. Шэнкс сделал ошибку в 527-м знаке, а потому и все последующие тоже были неправильными. Фергюсон провел последний год Второй мировой войны, вычисляя число π вручную, и к маю 1945 года достиг 530 знаков. К июлю 1946-го он дошел до 620, и более никто никогда не вычислял π с помощью лишь ручки и листа бумаги.