Алекс Беллос - Алекс в стране чисел. Необычайное путешествие в волшебный мир математики

Однако тонкая настройка гармонического ряда может оказаться еще более захватывающей. Мы произвольным образом решили удалить девятки. Если бы мы удалили из гармонического ряда все члены, содержащие 8, то оставшиеся члены также сходились бы к конечному числу, и то же самое повторилось бы при удалении всех членов, содержащих 7, и вообще любую выбранную цифру. На самом деле нет никакой необходимости ограничиваться отдельными цифрами. Удалим все члены, содержащие любое выбранное число, и «утоньшенный» таким способом гармонический ряд окажется сходящимся. Таким числом может быть, например, 9 или 42, или 666, или 314 159, — в каждом случае действует то же самое рассуждение.

Возьмем для примера число 666. В числах между 1 и 1000 сочетание цифр 666 встречается один раз. Между 1 и 10 000 оно встречается 20 раз, между 1 и 100 000 — 300 раз. Другими словами, процент его появления равен 0,1 % в первой тысяче чисел, 0,2 % — в первых 10 000 и 0,3 % — в первых 100 000. По мере перехода ко все большим и большим числам сочетание 666 будет встречаться все чаще и чаще. В конце концов окажется, что почти все числа содержат в себе 666. Стоит только выбросить их из гармонического ряда — и полученный «утоньшенный» ряд будет сходиться.

В 2008 году Томас Шмелцер и Роберт Бейли вычислили, что гармонический ряд, лишенный членов, содержащих число 314 159, суммируется к числу, немного превосходящему 2,3 миллиона. Это большое число, но ему ох как далеко до бесконечности.

Отсюда следует, что «гармонический ряд», состоящий из одних только членов, включающих сочетание цифр 314 159, должен суммироваться к бесконечности. Другими словами, ряд

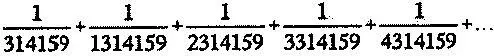
суммируется к бесконечности. Хотя он и начинается с очень маленького числа, и затем его члены становятся только меньше, сумма всех членов в конце концов преодолеет любое наперед заданное число. Причина, как и раньше, состоит в том, что, когда числа делаются очень большими, почти каждое число содержит в себе последовательность цифр 314 159. Почти все дроби с единичным числителем содержат 314 159 в знаменателе.

Напоследок взглянем на еще один бесконечный ряд, который тоже позволит нам прикоснуться к тайнам простых чисел. Простой гармонический ряд — это дроби с единичным числителем, знаменатели которых суть простые числа:

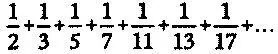
По мере увеличения чисел простые числа встречаются все реже и реже, так что можно было бы ожидать, что у этого ряда в конце концов не хватит сил, чтобы достичь бесконечности. Но — вы не поверите — он ее достигает! Этот впечатляющий результат, идущий вразрез с интуицией, заставляет нас осознать мощь и важность простых чисел. На них можно смотреть не только как на строительные элементы для натуральных чисел, но и как на строительные элементы, слагающие бесконечность.

Как-то раз, когда я был в гостях у Эдди Левина, дантиста на пенсии, он дал мне листок бумаги и попросил написать мое имя заглавными буквами. Левину 75 лет, у него чопорный вид, седые волосы топорщатся над продолговатым лбом. Он живет в северном Лондоне — на улице, которая является образчиком тех пригородов, где селятся преуспевающие и консервативные британцы. Я взял листок и написал: ALEX BELLOS.

Левин взял инструмент из нержавеющей стали, по виду напоминавший небольшую клешню с тремя зубцами. Твердой рукой он приложил ее к листу бумаги и принялся анализировать мою надпись. Он установил свой инструмент над буквой E в моем имени, при этом он был так сосредоточен, что ему позавидовал бы и раввин, делающий обрезание.

— Неплохо, — сказал он.

Этот инструмент — собственное изобретение Левина. Три зубца расположены так, что, когда инструмент раскрыт, их концы остаются на одной линии, причем расстояния между ними находятся в том же отношении друг к другу, как когда инструмент закрыт. Левин разработал его таким образом, что расстояние между средним и верхним зубцами всегда в 1,618 раз больше расстояния между средним и нижним. Поскольку данное число более известно как золотое сечение, он назвал свой инструмент калибром золотого сечения. (Среди других синонимичных названий числа 1,618 имеются золотая пропорция, божественная пропорция и φ, или фи.) Левин наложил свой калибр на написанную мной букву E так, чтобы кончик одного зубца пришелся на верхнюю горизонтальную черту в букве E, кончик среднего — на среднюю горизонтальную черту, а нижний оказался бы на нижней черте. Я полагал, что, выписывая заглавную букву E, я помещаю среднюю черту на равном расстоянии между верхом и низом, но калибр Левина продемонстрировал, что я бессознательно помещаю черту несколько выше середины — так, что она разбивает полную высоту буквы на два отрезка, отношение длин которых равно 1,618. Хотя я написал свое имя довольно небрежно, не успев ни о чем подумать, тем не менее оказалось, что я попал в число соблюдающих золотую пропорцию с поразительной точностью.

Левин улыбнулся и перешел к букве S. Он перенастроил свой калибр так, что зубцы касались самого верхнего и самого нижнего окончания буквы S, и, к моему полному изумлению, средний зубец попал точно на изгиб в букве S.

Точное попадание, — спокойно заметил Левин. — В почерк каждого человека заложена золотая пропорция.

Золотая пропорция — это число, которое описывает отношение, возникающее при делении отрезка на две части таким образом, что отношение всего отрезка к большему из двух равно отношению большего к меньшему. Другими словами, когда отношение А + В к А равно отношению А к В:

Деление отрезка на две части указанным образом называется золотым сечением. При этом число фи — отношение между большим и меньшим отрезками — можно вычислить, и оно равно (1 + 5√2√2√2√2)/2. Это иррациональное число, десятичное разложение которого начинается как

1,61803398874989484820…

Древних греков зачаровывало число фи. Они познакомились с ним, рассматривая пятиконечную звезду (пентаграмму), которая являлась почитаемым символом Пифагорейского братства. Евклид писал о «делении отрезка в крайнем и среднем отношении», он предложил метод построения правильного пятиугольника с помощью циркуля и линейки. Начиная с эпохи Возрождения это число интриговало как художников, так и математиков.