Виолетта Гайденко - Западноевропейская наука в средние века: Общие принципы и учение о движении

2) «сколько одно (x) приобретает, столько другое (y) утрачивает». Если эксплицировать пункты, выполнение которых подразумевается краткой формулировкой второго требования, то они состоят в следующем. Пусть движение х, у начинается в момент времени t 0, a U обозначает произвольный момент времени их движения. В момент t ix будет иметь скорость b i(b i> b), а у — скорость a i(a i< a). Тогда в соответствии со вторым требованием b i—b = a—a i.

Если с = (a – b)/2, т. е. является средним градусом широты, то x и y достигнут с одновременно, так что x и y будут иметь одинаковую скорость с в момент t k(t k= (t i– t 0)/2), где t i— момент окончания движения х, у. Точнее, если обозначить через

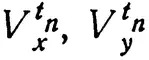
скорости x, y в момент времени t n, то

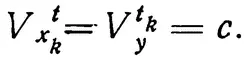
Отсюда

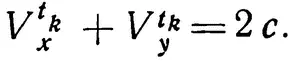
Но и для произвольного момента времени

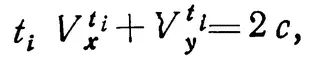
так как второе требование равносильно утверждению, что сумма скоростей x и y остается постоянной на протяжении всего движения.

Доказательством

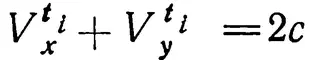
завершается, по существу, все доказательство теоремы у Суайнсхеда. Вывод о равенстве расстояний, проходимых при равноускоренном и равномерном движении со скоростью, равной среднему градусу широты первого, он считает столь очевидным, что предоставляет его сделать читателю. Действительно, из постоянства суммы скоростей V ti xи V ti y следует, что два равноускоренных движения, в результате которых проходится расстояние S = S x+ S y(S x, S y— расстояния, проходимые соответственно x и y), эквивалентны в отношении пройденного расстояния равномерному движению со скоростью V = 2c, продолжающемуся в течение того же времени. Поскольку S x= S y,то S xбудет пройдено за то же время при равномерном движении со скоростью с.

Быть может, самое любопытное в доказательстве Суайнсхеда — это то, что оно только отчасти является доказательством, а в гораздо большей степени — определением. Когда Суайнсхед указывает, что оба равноускоренных движения уменьшаются и возрастают равно быстро (equevelociter), то он считает возможным отсюда заключить, что «сколько одно приобретает, столько другое утрачивает». В действительности же только последнее уточнение придает утверждению о «равной быстроте» требуемую определенность. Суайнсхед считает необходимым как-то обосновать тот факт, что x и у одновременно достигнут среднего градуса с, что с не просто является полусуммой двух градусов a и b, но и расположено равно посередине, т. е. на равном удалении от а и b. В этом обосновании и состоит главная цель доказательства. Оно начинается с утверждения, что «все, составленное из двух неравных, является двойным по отношению к среднему между ними». В данном утверждении легко рассмотреть определение среднеарифметического, известное еще пифагорейцам, которые умели строить арифметические прогрессии, где каждый член является полусуммой двух соседних и одновременно отличается от них на одну и ту же величину (разность прогрессии). Суайнсхед, безусловно, все это знал и все же принимается снова доказывать, казалось бы, то же самое утверждение. Зачем? Ответ очевиден: он хотел математическое положение, касающееся чисел, представить в виде следствия кинематической теоремы. Его не удовлетворяет традиционное представление, поскольку в нем четко не разделяются два смысла, равно присущие термину «средний». Число l является «средним» (арифметическим) двух чисел k и m , если l , k, m рассматриваются, говоря современным языком, как конечные множества, сравниваемые между собой по количеству элементов, т. е. с точки зрения их мощности. Поэтому оно может быть названо «средним» в количественном смысле, поскольку l = (k + M)/2 означает, что l содержит вдвое меньше единиц, чем (k+m). С другой стороны, l можно получить из k и m , прибавляя или отнимая одно и то же число п. В этом случае l указывает границу двух элементарных шагов, с помощью которых можно перейти от k к т (или от т к k) : двухкратным прибавлением п к k (соответственно двухкратным вычитанием п из т). Число l как граница двух элементарных шагов может быть названо «средним» без какой-либо апелляции к количеству единиц, содержащихся в нем, независимо даже от того, представимо ли вообще оно в виде множества, — оно будет средним в порядке порождения, поскольку занимает среднее положение в порождаемой последовательности. Очевидно, что «среднее» по количеству и «среднее» по порядку, имея различные, причем независимые определения, совсем необязательно должны совпадать, точно так же, как количественные и порядковые характеристики вообще.

Движение, понятое как порождающий процесс, связывает в момент своей реализации оба вида величин воедино, или, если угодно, наоборот: интерпретация движения в виде процесса порождения заставляет ввести конструкцию, совмещающую в себе черты количественных и порядковых величин. Одной из самых смелых и глубоких интуиции мертонской школы было как раз открытие этой связи, и большое доказательство Суайнсхеда демонстрирует механизм, обеспечивающий совпадение среднеарифметического (a + b)/2 = c средним (в плане временной последовательности) положением с по отношению к а и b. Суайнсхед, как отмечалось, считал, что ему удалось доказать такое совпадение, показав, что оно является простым следствием равноускоренного движения. В мертонском определении равноускоренного движения не содержится ничего другого, кроме утверждения факта совпадения соотношений, характеризующих ряды количественных и порядковых величин. Равным приращениям времени сопоставляются равные приращения скорости, или в другой формулировке: если все время движения разделить на части, уменьшающиеся в непрерывной пропорции, то отношение скоростей на концах полученных временных отрезков будет описываться той же самой непрерывной пропорцией. Иначе говоря, указанное совпадение является синонимом равноускоренного движения, его нельзя ни вывести, ни доказать; его можно было только открыть.

б) Доказательство Уильяма Хейтсбери

В более раннем доказательстве теоремы о среднем градусе, принадлежащем Хейтсбери, разъяснению основных пунктов этого открытия посвящена значительная часть текста, причем у Хейтсбери еще более ясно, чем у Суайнсхеда, выражено стремление доказать эти пункты.