Владимир Бердников - Эволюция и прогресс

Так как направление сдвига частоты аллеля А 1 сохраняет свою полную неопределенность и в последующих поколениях, то средняя частота этого аллеля <���р 2> в совокупности популяций второго поколения не должна отличаться от < р 1 >. Отсюда мы приходим к выводу, что в любом поколении средняя частота аллеля в совокупности популяций, происходящих от какой-то одной, остается равной частоте этого аллеля в исходной популяции, т. е.

р 0= <���р 1> = <���р 2> =… (3.25)

Несмотря на то что в каждой популяции динамика изменения аллельных частот непредсказуема, мы можем с полной уверенностью утверждать, что рано или поздно такие изменения прекратятся. Могут быть только два финала: или частота аллеля возрастет до единицы, или она опустится до нуля. Достижение нуля означает потерю аллеля, а достижение единицы — его фиксацию. На рис. 11 приведено несколько судеб нейтральных аллелей, смоделированных компьютером. Каждая траектория частоты аллеля заканчивается либо нулем, либо единицей. Случайный характер изменения аллельной частоты напоминает движение броуновской частицы в трубке, на концы которой помещено клейкое вещество. Очевидно, что при своем блуждании частица когда-нибудь достигнет одного из концов трубки и там приклеится (зафиксируется). Итак, генный дрейф «стремится» уменьшить разнообразие аллелей, одна их часть теряется, а другая фиксируется.

Теперь рассмотрим совокупность всевозможных финалов частоты аллеля А 1 . У части финальных популяций она будет равна единице, а у всех других — нулю. Очевидно, что доля популяций, зафиксировавших в конце концов аллель А 1 (иначе говоря, вероятность фиксации данного аллеля), равна его средней частоте в полной совокупности финальных популяций. Поскольку (см. формулу (3.25)) последняя должна равняться частоте аллеля в исходной популяции ( р 0 ), мы приходим к нетривиальному заключению: вероятность фиксации нейтрального аллеля равна его частоте в генофонде популяции. Например, если эта частота равна 0,5, то аллель с равной вероятностью может или исчезнуть из популяции, или в ней зафиксироваться. Теперь перейдем к очень важному следствию — к судьбе только что возникшей мутации.

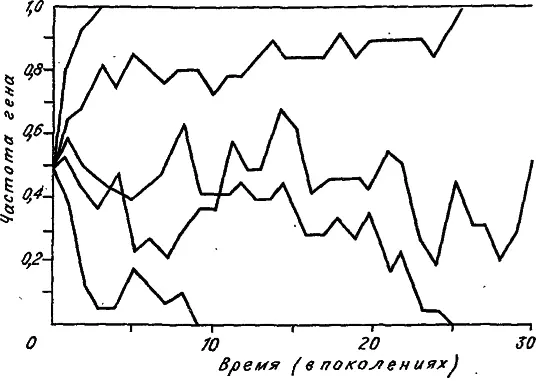
Рис. 11. Дрейф аллельных частот в пяти машинных экспериментах. Размер популяции N = 10. Исходная частота обоих аллелей 0,5 (по: [Kimura, 1983]).

Пусть в популяции возник совершенно новый нейтральный аллель. Очевидно, что его частота в момент возникновения равна 1/2 N, поэтому и зафиксироваться с помощью дрейфа он может с той же вероятностью. Этот результат приводит нас к грустному выводу: фактически любой вновь возникший аллель обречен на исчезновение, поскольку вероятность этого события чрезвычайно близка к единице (1 — 1/2 N ). В то же время заметим, что процесс мутирования постоянно ведет к появлению новых аллелей. Если через V обозначить мутабильность локуса, то в каждом поколении в популяции должно появляться 2 NV мутантных аллелей. Поскольку они не различаются естественным отбором, любой из них может зафиксироваться с вероятностью 1/2 N. Значит, в данном случае скорость фиксации любого мутантного аллеля только за счет генного дрейфа должна равняться 2NV(1/2N). Обозначив скорость фиксации мутантного аллеля через К, приходим к очень простому уравнению

K = V. (3.26)

Этот изящный результат, полученный М. Кимурой в 1960 г., показывает, что в популяциях (вне зависимости от их размеров) может идти процесс фиксации новых аллелей, скорость которого определяется только скоростью мутирования локусов. Однако среднее число поколений, нужное для фиксации мутантного аллеля с помощью дрейфа, пропорционально размеру популяции и, как показал Кимура, оно близко к 4 N.

Заметим, что геном любого вида содержит несколько тысяч локусов, поэтому в генофонде любой популяции только вследствие неизбежного генного дрейфа почти в каждом поколении фиксируются какие-то аллели. Однако подчеркнем, что этот вывод мы получили при допущении, что жизнеспособность организма не зависит от аллельного состава локусов; иными словами, естественный отбор эти аллели не различает. Несмотря на то что фиксация нейтральных аллелей занимает много времени, у данного процесса есть одна выгодная для популяции особенность — он проходит для нее совершенно бескровно.

Движущий отбор

До сих пор мы имели дело с панмиктической популяцией конечного размера, занимающей ограниченную территорию с фиксированными условиями среды. На самом же деле мир, в котором обитает популяция, изменчив, и идеально приспособиться к нему невозможно. Представим себе, что наша популяция в какой-то момент времени хорошо приспособлена к условиям своего существования, однако вдруг эти условия начали медленно, но неуклонно ухудшаться. В данной ситуации перед популяцией встает проблема огромной сложности: нужно не просто отбраковать относительно редкие мутантные аллели (чему в немалой степени помогает генетический дрейф), но и заменить старые, далеко не дефектные аллели на иные, более благоприятные, т. е. лучше соответствующие новым условиям среды.

Будем считать, что благоприятные мутации полудоминантны, т. е. h = 0,5. Если принять приспособленность гомозигот по старому аллелю ( w 11 ) за единицу, то приспособленность гомозигот по благоприятному аллелю ( w 22 ) должна равняться ( 1+s ), а гетерозигот — ( 1+0,5s ). По аналогии с рассмотренным выше случаем вредных мутаций, заменяя — s на +s, можно рассчитать среднюю приспособленность популяции ( w ) и среднюю приспособленность доноров благоприятного аллеля ( w 2 ):

w = 1 + qs, (3.27)

w 2= 1 + 0 ,5ps + qs , (3.28)

тогда сдвиг частоты благоприятного аллеля за одну генерацию можно определить по формуле

Δq = (0,5pqs) / (1 + qs). (3.29)

При малых значениях q и s знаменатель в правой части этого уравнения мало отличается от единицы, поэтому с хорошей точностью должно выполняться соотношение

Δq ≈ 0,5pqs , (3.30)

т. е. скорость возрастания частоты благоприятного аллеля в генофонде популяции прямо пропорциональна его частоте и селективному преимуществу.

Глядя на соотношение (3.30), можно подумать, что были бы в наличии благоприятные мутации, а процесс их фиксации — дело десятое. Однако анализ решения этого уравнения показывает, что даже при таком высоком коэффициенте отбора, как 0,1, для достижения частот благоприятного аллеля, близких к единице, требуется около 100 поколений, при s = 0,01 — не менее 1000.