Владимир Бердников - Эволюция и прогресс

N = N 11+ N 22+ N 12 . (3.1)

Каждая особь вносит в генофонд популяции два экземпляра гена А , или (выражаясь несколько иначе) каждая особь является донором (или поставщиком) двух экземпляров этого локуса. Гомозиготы А 1А 1 вносят 2 N 11 копий аллеля А 1 , гомозиготы А 2А 2 — 2 N 22 копий аллеля А 2 , тогда как гетерозиготы А 1А 2 — 2 N 12 копий аллеля А 1 и столько же копий аллеля А 2 . Отсюда легко оценить долю (частоту) каждого аллеля среди всех 2N экземпляров локуса А , которыми располагает генофонд популяции. Обозначим частоту аллеля А 1 через р, а частоту аллеля А 2 через q (отметим, что р + q = 1). Эти частоты можно вычислить по формулам

p = (2N 11+ N 12) / 2N = (N 11+ 0,5N 12) / N , (3.2)

q = (2N 22+ N 12) / 2N = (N 22+ 0,5N 12) / N . (3.3)

Гетерозиготы являются донорами сразу двух аллелей, в связи с этим (чисто формально) можно считать, что одна половина гетерозигот вносит в генофонд аллель А 1 , а другая — аллель А 2. Тогда всех особей популяции можно представить в виде суммы двух классов — доноров аллеля А 1 с численностью N 1 и доноров аллеля А 2 с численностью N 2. При этом

N 1= N 11+ 0,5N 12, (3.4)

N 2= N 22+ 0,5N 12. (3.5)

Взглянув на правые части равенств (3.2) и (3.3), мы видим, что в популяции частота каждого аллеля равна доле его доноров:

p = N 1/ N; q = N 2/ N. (3.6)

Рассмотрим популяцию на двух стадиях развития ее особей — на стадии зиготы и взрослого организма. Обозначим численность зигот через N, а численность взрослых — через N'. Каждая из этих величин (N и N') складывается из численностей трех генотипических классов: N 11, N 22, N 12 — для зигот и N 11', N 22', N 12' — для взрослых. Теперь каждому генотипическому классу припишем его приспособленность: w 11— гомозиготам A 1A 1, w 22— гомозиготам А 2А 2 и w 12 — гетерозиготам. Определим приспособленность каждого генотипа как долю зигот (с данным генотипом), достигших взрослой стадии, т. е.

w 11= N' 11/ N 11; w 12= N' 12/ N 12; w 22= N' 22/ N 22 . (3.7)

Так же можно ввести представление и о приспособленности любой группы генотипов. Например, можно говорить о средней приспособленности популяции ( w ) как о доле всех зигот, успешно завершивших развитие. Аналогично определяется средняя приспособленность доноров каждого аллеля — w 1и w 2:

w = N' / N; w 1= N 1' / N 1; w 2= N 2'/ N 2 . (3.8)

Наша главная задача состоит в том, чтобы определить, как под действием отбора изменяется аллельный состав популяции, иначе говоря, как изменяется частота аллелей А 1 и А 2 за время онтогенеза особей.

Доля аллеля в генофонде популяции равна доле его доноров (формулы (3.6)). В случае аллеля А 2 это ( N 2/ N ) — на стадии зигот и ( N 2' / N' ) — на стадии взрослых. Поэтому сдвиг частоты аллеля А 2 в результате отбора ( Δq ) можно получить как разность: ( N 2' / N' ) — ( N 2/ N ). Выразив численности взрослых через численности зигот (см. уравнения (3.8)), получим

Δq = N 2*w 2/ Nw — N 2/ N = q((w 2— w) / w) . (3.9)

Итак, сдвиг частоты аллеля в генофонде популяции в результате отбора равен частоте этого аллеля до отбора, умноженной на относительное превосходство приспособленности его доноров над средней приспособленностью популяции.

Отбор в панмиктической популяции

Перейдем к панмиктической популяции. Здесь при оплодотворении аллели гамет соединяются в генотипы зигот по правилам свободного попарного комбинирования. Зиготы с генотипами А 1А 1, А 1А 2 и возникают в соотношениях р 2: 2pq: q 2 (рис. 10). Эти же соотношения, получившие название закона Харди-Вайнберга, будут справедливы и для взрослых членов популяции, если приспособленность всех генотипов одна и та же. Закон Харди-Вайнберга довольно часто выполняется в природных популяциях, он позволяет легко вычислять частоты генотипов, исходя из частот аллелей.

В нашей модели отличия в приспособленности особей обусловлены только разным уровнем их жизнеспособности, поэтому численности зигот трех генотипических классов А 1А 1, А 1А 2 и А 2А 2 соответственно равны Np 2, 2Npq и Nq 2. Тем самым зиготы в точности отражают генофонд популяции взрослых особей предыдущего поколения. В результате действия отбора численности генотипов взрослых особей, развившихся из зигот, приобретают вид

N 11' = Np 2w 11; N 12' = 2Npqw 12; N 22' = Nq 2w 22 . (3.10)

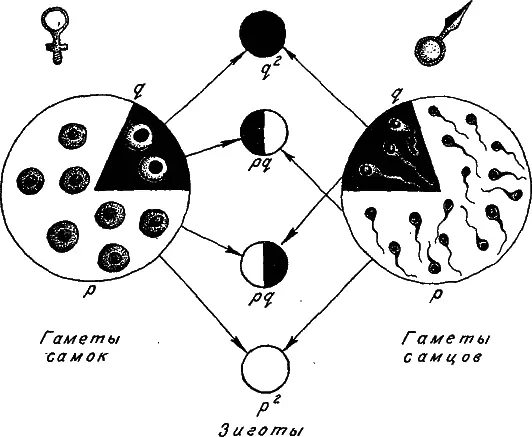
Рис. 10. Схема формирования генотипов зигот при случайном соединении гамет (при панмиксии).

Объяснения в тексте.

Численность всех взрослых особей после отбора связана с численностью зигот уравнением

N' = N(р 2w 11+ 2pqw 12+ q 2w 22). (3.11)

Поскольку отношение N'/N выражает среднюю приспособленность популяции (см. уравнения (3.8)), поделив обе части уравнения (3.11) на N, получим

w = р 2w 11+ 2pqw 12+ q 2w 22 . (3.12)

По аналогии с формулой (3.5) можно получить численность доноров аллеля А 2 после отбора, т. е. среди взрослых потомков

N 2' = N 22' + 0,5N 12' , (3.13)

или, учитывая соотношения (3.10),

N 2' = Nq 2w 22+ Npqw 12 . (3.14)

Поделив обе части этого уравнения на N 2= Nq (см. (3.6)), получим значение приспособленности доноров аллеля А 2 :

w 2= N 2' / N 2= (Nq(qw 22+ pw 12)) / Nq , (3.15)

т. е.

w 2= pw 22+ qw 12 .

Точно так же можно показать, что

w 1= pw 11+ qw 12 . (3.16)

Итак, мы располагаем всеми данными для вычисления сдвига частот аллелей после отбора (см. уравнение (3.9)).

Отбор в смысле Ч. Дарвина основан не на абсолютном уровне истребления молодых особей, а на различиях в степени такого истребления. В связи с этим приспособленность какой-то группы особей удобно объявить равной единице, а приспособленность других групп представить в виде суммы 1 + s (s — коэффициент отбора). Такой прием позволяет рассмотреть наиболее интересную для нас задачу — судьбу мутаций, влияющих на относительную приспособленность их носителей.

Судьба вредной мутации

Предположим, что в огромной панмиктической популяции возник и каким-то образом распространился новый аллель А 2 локуса А. (Ранее этот локус был представлен аллелем А 1.) Ясно, что мутантный аллель может встречаться в гомо- и гетерозиготном состояниях. Если мутация вредная, значит, приспособленность гомозигот А 2А 2 должна быть ниже, чем у гомозигот по нормальному аллелю А 1 А 1. Это обстоятельство мы можем отразить равенствами w 11 = 1, w 22 = 1— s. Возникает вопрос: какая приспособленность будет у гетерозигот А 1 А 2?

В классической генетике рассматриваются три случая: 1) мутация рецессивна, т. е. приспособленность гетерозигот равна приспособленности гомозигот по нормальному аллелю w 12= w 11= 1; 2) мутация доминантна, т. е. приспособленность гетерозигот равна приспособленности гомозигот по мутантному аллелю w 22= w 12= 1—s; 3) случай неполного доминирования, когда приспособленность гетерозигот ниже, чем у гомозигот по нормальному аллелю, но выше, чем у гомозигот по мутантному. Степень доминирования можно оценить с помощью специальной величины А, варьирующей от нуля до единицы. При этом приспособленность гетерозигот можно выразить формулой w 12= 1 — hs, охватывающей все три рассмотренных выше случая. При h = 0 мы имеем дело с рецессивной вредной мутацией, при h = 1 — с доминантной, а при неполном доминировании — 0 < h < 1.