Журнал «Открытия и гипотезы» - Открытия и гипотезы, 2015 №04

В Египте нашли применение только аликвотные дроби (числитель равный единице, и знаменатель любое натуральное число), а все остальные дроби разлагались на сумму аликвотных. В папирусе Ахмеса представлены таблицы таких разложений для дробей.

При определении площади квадрата, объёма куба или нахождении стороны квадрата по его площади египтяне сталкивались с возведением в степень и извлечением корня, хотя названий этих операций ещё не было.

Зарубки на кости, возможно, отображающие счёт, найдены около озера Эдуард (Центральная Африка) имеют возраст более 30 тысяч лет.

Часть папируса египетского писца Ахмеса(XVIII–XVII века до н. э.)

Вавилонские клинописные математические тексты использовали шестидесятеричную систему счисления, характерную ещё для шумер, и представляли собой учебные пособия, которые включали таблицы умножения для чисел от 1 до 59, а также таблицы обратных чисел, таблицы квадратов и кубов чисел натурального ряда, таблицы вычисления процентов, дроби с основанием 60. Известно более трёхсот табличек с текстами математических задач и числовыми таблицами. Для Вавилона вообще характерно широкое применение таблиц.

Здесь впервые появляется последовательная позиционная нумерация. Первые пятьдесят девять чисел записывались с повторением знаков единиц и десятков нужное число раз. Аналогичным образом записывались числа, кратные шестидесяти.

Кроме того, вавилоняне ввели знак, обозначающий ноль при записи числа.

Сложение и вычитание в Вавилоне были аналогичны данным действиям в десятичной позиционной системе с тем отличием, что переход в следующий разряд был необходим как для основания системы, так и для единиц и десятков.

Из-за большого основания вавилоняне пользовались не единой таблицей умножения до 59, которая бы содержала большое число элементов, а множеством таблиц произведений чисел от 1 до 59.

Операции деления у вавилонян не было, поэтому большое внимание было уделено составлению таблицы обратных величин, то есть чисел, образующихся при делении 60 на 2,3,4…

В случае деления, дающего бесконечную дробь, сначала писалось, что обратного числа нет, а позднее стало даваться приближённое значение.

Вавилонская табличка с вычислением.

Вавилонские цифры.

Пожалуй, ни один из народов не дал больше для развития арифметики, чем греки. Первоначально эллины пользовались аттической нумерацией, которая использовала знаки для чисел 1, 5, 10, 50, 100, 500, 1000. Эту систему описал грамматик и историк Геродиан во II веке н. э. С её помощью результаты вычислений выписывались на счётной доске — абаке.

Со временем аттическую нумерацию заменила компактная буквенная, или ионическая. Она использовала 24 буквы греческого алфавита и три вышедшие из обращения буквы для обозначения единиц от 1 до 9, десятков от 10 до 90 и сотен от 100 до 900. Чтобы отличать числа от букв над ними ставили черту. Для записи числа 1000 использовали тот же символ, что и для единицы, но со штрихом слева снизу.

Развитие древнегреческой арифметики связано с пифагорейской школой. Пифагорейцы полагали поначалу, что отношение любых двух отрезков можно выразить через отношение целых чисел, то есть геометрия представляла собой арифметику рациональных чисел.

Использование аналогичных отношений в гармонии и музыке привело пифагорейцев к выводу, что все закономерности мира можно выразить с помощью чисел, а арифметика нужна для того, чтобы сформулировать отношения и построить модель мира.

В частности, пифагореец Архит писал: «Арифметика, по [моему] мнению, среди прочих наук весьма выделяется совершенством знания; да и геометрии [она совершеннее, так как] она яснее, чем геометрия, рассматривает любой [предмет]».

Пифагорейцы рассматривали только целые положительные числа и полагали число собранием единиц. Единицы были неделимы и располагались в виде правильных геометрических тел. Пифагорейцам характерно определение «фигурных чисел» («треугольных», «квадратных» и других). Изучая свойства чисел, греки разбили их на чётные и нечётные (как признак делимости на два), простые и составные.

Известно, что у пифагорейцев существовало учение о рациональных числах, или отношениях отрезков, но само оно не сохранилось. Вместе с тем им принадлежит доказательство несоизмеримости диагонали и стороны единичного квадрата. Данное открытие означало, что отношений целых чисел недостаточно для выражения отношений любых отрезков и что на этом основании невозможно строить метрическую геометрию.

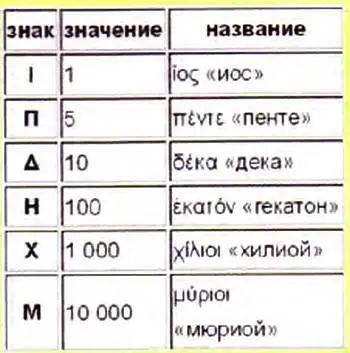
Аттическаясистема счисления — непозиционная система счисления, применявшаяся в древней Греции до III века до н. э.

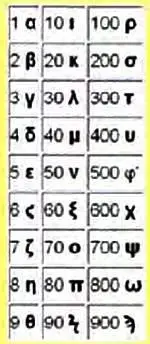
Ионийская— непозиционная система счисления. Алфавитная запись чисел, пришедшая на смену аттической, в которой в качестве символов для счёта, употребляют буквы классического греческого алфавита.

Рафаэль Санти. Афинская школа.

В Греции также умели оперировать дробями вида m/n, складывать и вычитать их, приводя к общему знаменателю, умножать и делить, а также сокращать. В теоретических построениях греки исходили из неделимости единицы и говорили не о долях единицы, а об отношении целых чисел. Для этих отношений было определено понятие пропорциональности, которое разбивало все отношения на непересекающиеся классы.

После завоеваний Александра Македонского центр греческой науки сместился в Александрию. Основополагающим трудом того времени являются «Начала» Евклида, состоящие из тринадцати книг. Книга V посвящена теории отношений Евдокса, книга VI — связи отношений с операцией умножения отрезков, или построению параллелограммов, книги VII–IX — теории целых и рациональных чисел, также рассматриваемых как отрезки, книга X — классификации иррациональностей по Теэтету.

В работе Архимеда «Псаммит» был разработан метод для выражения сколь угодно больших чисел. Он показал, что число песчинок в сфере, диаметр которой менее чем в 10000 раз превосходит диаметр Земли, не превышает 10 63, иными словами является конечным.