Антонио Дуран - Истина в пределе. Анализ бесконечно малых

тригонометрических функций:

логарифмов:

показательных функций:

а также правила вычисления производной для основных операции с функциями, в частности суммы:

произведения:

деления:

и для сложных функций:

Гордиевым узлом анализа бесконечно малых на протяжении XVII, XVIII и начала XIX века оставалось четкое определение того, как следует понимать значение дроби

при h = 0. Этот гордиев узел разрубил французский математик Огюстен Луи Коши (1789—1857), применив понятие предела, которое он сам же и определил более или менее точно и которое затем улучшил немецкий математик Карл Вейерштрасс (1815—1897). Об этом рассказывается в главе 6.

Так как мгновенная скорость, с которой движется тело, является производной, то трудности при делении ноля на ноль препятствовали развитию физики, пока Ньютон не решил эту проблему, создав анализ бесконечно малых. До конца XVII века, когда был сформирован анализ бесконечно малых, ученые могли изучать только простейшие виды движения: равномерное движение, при котором пройденный путь пропорционален затраченному времени, следовательно, скорость постоянна, а ускорение отсутствует, а также равноускоренное движение, при котором пройденный путь пропорционален квадрату времени, скорость пропорциональна времени, а ускорение постоянно. Для изучения последнего вида движения, примером которого является падение тела под действием силы тяжести, потребовался гений Галилея, который понял его суть за несколько десятков лет до того, как с помощью анализа бесконечно малых было найдено тривиальное решение этой задачи.

Проиллюстрируем это на примере. Рассмотрим, как и в прошлых примерах, движущееся тело, которое в момент времени t прошло расстояние в s(t) = √t. Время будем измерять в секундах, расстояние — в метрах. Вычислить среднюю скорость движения тела несложно: например, в период времени с первой по четвертую секунду средняя скорость будет равна отношению пройденного пути и затраченного времени:

Но что, если нас интересует не средняя скорость, а мгновенная скорость в конкретный момент времени? Чтобы упростить рассуждения, допустим, что мы хотим вычислить мгновенную скорость в тот момент, когда проходит ровно одна секунда от начала движения. Выберем приращение времени h и вычислим среднюю скорость в интервале времени от 1 секунды до (1 + h) секунд:

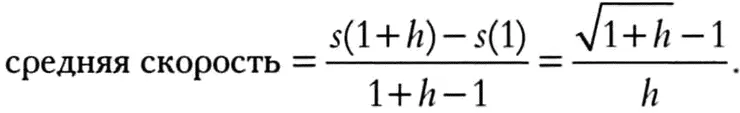
Чтобы вычислить мгновенную скорость в первую секунду, достаточно свести приращение времени h к нулю. Однако в этом случае снова возникает неопределенность:

Это происходит потому, что мгновенная скорость соответствует значению производной функции пройденного пути s(t) = √t. в момент времени t = 1.

В предыдущей таблице с числами указано, что значение этой производной должно равняться 0,5. Покажем, что это и в самом деле так, устранив неопределенность следующим способом:

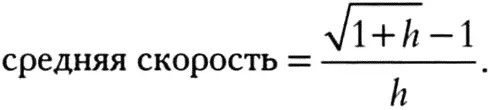
Умножим числитель и знаменатель на √(1+h) + 1и упростим выражение:

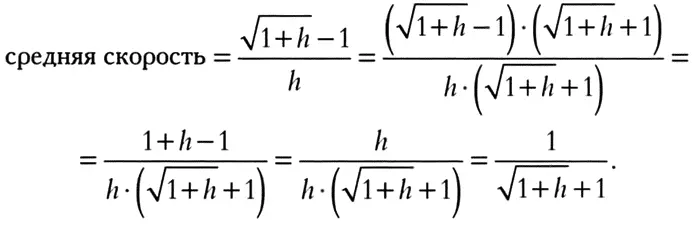
Если в последнем выражении свести приращение времени h к нулю, то мы уже не столкнемся с неопределенностью и делением на ноль. Как и следовало ожидать, при h = 0 значение дроби будет равно 0,5. На языке физики это означает:

Следовательно, мы устранили изначальную неопределенность, которая возникает из-за деления ноля на ноль, и получили, что если тело проходит за t секунд √ t метров, то по прошествии 1 секунды оно будет двигаться со скоростью 1/ 2м/с.

Другим базовым понятием анализа бесконечно малых является понятие интеграла. Интеграл используется для вычисления площади, ограниченной графиком функции.

Например, пусть дана функция f, определенная на интервале между а и b. Значение интеграла

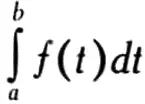
будет равно площади следующей фигуры:

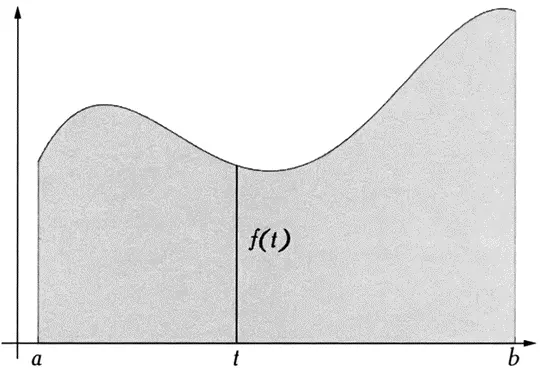
Символ ∫ для обозначения интеграла придумал Лейбниц (об этом подробно рассказывается в главе 4). Этот символ представляет собой стилизованную букву S — первую букву латинского слова summa («сумма»).

Интеграл применяется не только для вычисления площадей: в математике он также используется для расчета объемов, длин и определения центра тяжести. В физике ему соответствует понятие работы. Работа, которую необходимо совершить,. чтобы переместить тело под действием силы f из точки а в точку b , рассчитывается по формуле:

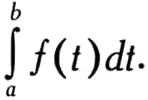
Интеграл также используется для расчета пройденного телом пути, если известна скорость тела. Рассмотрим в качестве примера физическую задачу, о которой мы говорили в самом начале этой главы: какой путь пройдет тело спустя 4 секунды после начала движения, если в течение t секунд оно двигалось со скоростью, равной t 2м/с? Ответ вычисляется по следующей формуле:

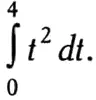
Задача сводится к вычислению этого интеграла. Если интерпретировать интеграл как площадь фигуры, он будет соответствовать площади, ограниченной участком параболы. Эту площадь вычислил Архимед еще 2300 лет назад. Это открытие наряду с другими принесло ему вечную славу: Архимеда по праву можно считать одним из величайших основателей интегрального исчисления (об этом более подробно рассказывается в главе 2).

Строгое определение интеграла, в котором не участвует понятие площади, — непростой вопрос с точки зрения логики. Здесь, пусть и в несколько иной форме, в дело снова вступают бесконечно малые величины. Из рисунка на предыдущей странице видно, что искомая фигура состоит из отрезков длиной f(t), где t принимает все возможные значения на интервале от а до b. Площадь искомой фигуры представляет собой сумму «площадей» этих отрезков. Однако эти отрезки имеют нулевую ширину, поэтому может показаться, что они не имеют площади. Мы вновь сталкиваемся с понятием бесконечно малой величины — ширины этих отрезков. В нотации, придуманной Лейбницем для обозначения интегралов, площадь фигуры, ограниченной кривой, понимается как сумма бесконечно малых: согласно рисунку на предыдущей странице, все отрезки, образующие фигуру, имеют высоту f(t).