Антонио Дуран - Истина в пределе. Анализ бесконечно малых

Согласно Лейбницу, бесконечно малая ширина обозначается dt. Площадь этих «отрезков» равна произведению их основания на высоту, то есть f(t) dt, а площадь фигуры, которую мы хотим вычислить, равна сумме этих площадей: ∫ f(t)dt.

Смысл этой суммы так и не смогли объяснить ни Ньютон, ни Лейбниц, создатели анализа бесконечно малых. По сути, первое точное определение интеграла было дано почти полтора столетия спустя усилиями Коши. В нем также используется понятие предела (более подробно об этом рассказывается в главе 6).

Вычисление площадей криволинейных поверхностей — очень сложная задача, в чем на собственном опыте убедились предшественники Ньютона и Лейбница. В некотором смысле эта задача аналогична задаче о вычислении интеграла. Вычисление интегралов во многих случаях (но не всегда) упрощает основная теорема анализа.

Анализ бесконечно малых — своеобразный мост между производными и интегралами: основная теорема анализа гласит, что интегрирование и вычисление производной являются взаимно обратными операциями. Точнее говоря, если мы хотим вычислить интеграл

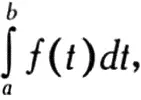
то, согласно основной теореме анализа, достаточно найти функцию F такую, что

для любого t в интервале между а и b. В этом случае

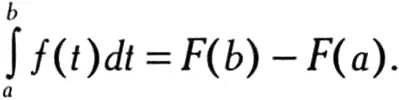
Функция f должна обладать еще одним свойством — непрерывностью, на котором мы не будем останавливаться подробно.

Рассмотрим на примере, как основная теорема анализа упрощает вычисление интеграла

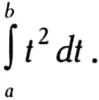
Этот интеграл в зависимости от его интерпретации можно использовать для расчета площади, ограниченной параболой; площади, ограниченной спиралью Архимеда; а также пути, пройденного телом, которое движется со скоростью v(t) = t 2.

Согласно основной теореме анализа, достаточно найти функцию, производной которой будет функция t 2. Это нетрудно сделать с помощью правила вычисления производной степенной функции:

Тогда

Отсюда нетрудно вывести, что производная функции t 3/3 в точности равна t 2. Следовательно:

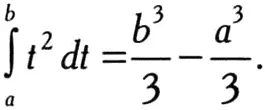
Как мы уже упоминали выше, путь, пройденный за 4 секунды телом, которое в течение t секунд движется со скоростью t 2, определяется интегралом:

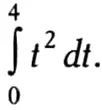
Следовательно, достаточно подставить в предыдущую формулу а = 0 и b = 4:

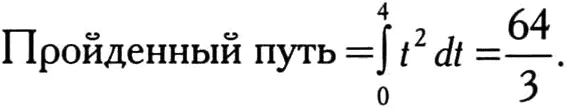
Рассмотрим спираль Архимеда — кривую, получаемую равномерным движением точки вдоль луча, который, в свою очередь, равномерно вращается вокруг своего начала. Будем считать, что точка движется вдоль луча со скоростью 1м/с, скорость вращения луча постоянна. Чтобы найти площадь, ограниченную первым витком спирали Архимеда, нужно вычислить интеграл

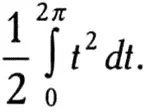
Достаточно подставить в предыдущую формулу а = 0 и b = 2π

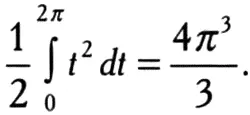
Именно этот результат получил сам Архимед, который изложил его иначе: «Площадь первого витка спирали равна трети площади круга, радиус которого равен длине пути, пройденного точкой вдоль прямой во время первого витка». В самом деле, так как на первом витке спирали точка проходит вдоль прямой путь, равный 2π, круг этого радиуса будет иметь площадь p ∙ (2π) 2= 4π 3, о чем пишет Архимед.

Автор этой книги не ставил перед собой задачу подробно рассказать о понятиях и методах анализа бесконечно малых. Намного интереснее то, каким образом математики открыли эти понятия и как они изменялись со временем. В следующих главах мы расскажем об интеллектуальной эпопее длиной почти в две тысячи лет. Читатель узнает, как Ньютон, Лейбниц, Эйлер, Коши и другие великие математики создавали и последовательно видоизменяли понятия дифференциала, производной, интеграла и предела, пока они не приобрели тот вид, в котором известны нам сегодня.

В течение всего процесса формирования анализа бесконечно малых, длившегося почти две тысячи лет, со времен Архимеда до эпохи Ньютона и Лейбница, было создано множество различных математических теорий и концепций. Было вновь открыто и осмыслено наследие древних греков, в особенности работы Архимеда; появилась более сложная система счисления, чем древнегреческая и римская; и, разумеется, возникла алгебра и аналитическая геометрия, позволившая использовать методы алгебры при работе с кривыми. Стало возможным решать задачи о касательных, вычислении площади, центров тяжести, максимумов и минимумов и подобные им алгебраическим путем. Алгебра и аналитическая геометрия, по сути, стали тем языком, на котором можно было описать ранние этапы развития математического анализа. Это случилось благодаря усилиям плеяды ученых, которые совершили множество важных открытий, особенно в XVII веке.

Этот процесс был очень сложным, интенсивным и интересным не только с научной, но и в большей степени с исторической точки зрения. На него влияли крупнейшие события в истории человечества, которые, в частности, привели к утрате классической греческой культуры и последующему возврату к ней, к научно -технической революции. Сказались на формировании этого раздела математики и проблемы обособленности, вызванные сложной политической ситуацией и многочисленными войнами в Европе в XVII веке. Не обошлось и без влияния интриг одних ученых против других, непримиримых споров, диспутов и оскорблений.

Мы начнем наш рассказ с экскурса в Древнюю Грецию. Именно тогда математики и философы предприняли первые попытки понять бесконечность — метафизическую основу математического анализа.

Для древних греков бесконечность была двухголовым монстром: с одной стороны — бесконечно малое, с другой — бесконечно большое. Бесконечность вскоре оказалась вовлечена в скандалы и споры. В некотором роде она проявилась в невозможности измерить одной мерой сторону квадрата и его диагональ, что разрушило пифагорейскую концепцию вселенной и привело к первому фундаментальному кризису в математике. Она также присутствовала в апориях Зенона о движении и множестве, в которых, помимо прочего, проявлялось диалектическое противоречие между различными философскими течениями той эпохи. Апории Зенона также показывают влияние этих противоречий на математику.