Журнал «Открытия и гипотезы» - Открытия и гипотезы, 2015 №05

То есть существует какая-то минимальная размерность гиперкуба, при которой условие нарушается, и уже невозможно избежать комбинации раскраски отрезков, где четыре точки одного цвета будут лежать в одной плоскости. И эта минимальная размерность точно больше шести и точно меньше числа Грэма, в этом и заключается математическое доказательство ученого.

А теперь определение того, что я выше расписал на несколько абзацев, сухим и скучным языком математики.

В 1971-м году Грэм доказал, что указанная проблема имеет решение, и что это решение (количество размерности) лежит между числом 6 и неким большим числом, которое позже (не самим автором) было названо в его честь. В 2008-м году доказательство улучшили, нижнюю границу подняли, теперь искомое количество размерностей лежит уже между числом 13 и числом Грэма. Математики не спят, работа идет…

С 70-х годов прошло немало лет, были найдены математические задачи, в которых проявляются числа и побольше грэмова, но это первое число-монстр так поразило современников, понимавших о каких масштабах идет речь, что в 1980-м году его включили в книгу рекордов Гиннесса, как «самое большое число, когда-либо участвовавшее в строгом математическом доказательстве» на тот момент.

Давайте попытаемся разобраться, насколько оно велико. Самое большое число, могущее иметь какой-то физический смысл 10 185, а если всю Обозримую Вселенную заполнить кажущимся бесконечным набором мизерных циферок, получим что-то соизмеримое с гуголплексом.

Представляете себе эту громаду? Вперед, назад, вверх, вниз, насколько хватает глаз и насколько хватает телескопа Хаббл, и даже насколько не хватает, до самых далеких галактик и заглядывая за них — цифры, цифры, цифры размером много меньше протона.

Число действительно огромно, рвет мозг. Число содержит 10 185цифр, его можно изобразить как 10 10 в степени 185.

Раскроем двери восприятия чуть пошире. Помните инфляционную теорию? Что наша Вселенная лишь одна из многих пузырьков Мультивселенной. А если представить 10 10 в степени 185таких пузырьков?

Представим себе Мультивселенную с подобным количеством вселенных, каждая из которых под завязку исписана цифрами — получим 10 10 в степени 185х 10 10 в степени 185. Представляете себе такое?

Но даже это не идёт ни в какое сравнение с числом Грэма. Если его представить в виде палки, растянутой во всю Обозримую Вселенную, то, 10 10 в степени 185х 10 10 в степени 185окажется засечкой толщиной недостойной упоминания.

Мультивселенная, где каждый пузырёк представляет собой отдельную вселенную.

Тут возникает проблема — как же число Грэма записать на бумаге? Для этого существует так называемая стрелочная нотация Кнута.

Начнём с мелочи. Например g1 = З↑↑↑↑З

Что это значит? Одна стрелочка означает обыкновенное возведение в степень.

2↑2 = 2 2= 4

З↑З = З 3= 27

4↑4 = 4 4= 256

10↑10 = 10 10= 10 000 000 000

Две стрелочки означают возведение в степень степени.

Короче говоря, «число стрелочка стрелочка другое число» показывает, какая высота степеней (математики говорят «башня») выстраивается из первого числа.

Например. 5↑↑8 означает башню из восьми пятерок и настолько велико, что не может быть рассчитано ни на каком суперкомпьютере, даже на всех компьютерах планеты одновременно.

Переходим к трем стрелочкам. Если двойная стрелочка показывала высоту башни степеней, то тройная, казалось бы, укажет «высоту башни высоты башни»?

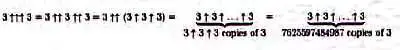
Какой-там! В случае тройки мы имеем высоту башни высоты башни высоты башни.

То есть З↑↑↑З образует башню из троек, высотой в 7 триллионов штук. Если вы внимательно читали этот текст и не уснули в самом начале, вероятно помните, что от Земли до Сатурна 100 триллионов сантиметров. Значит, башня из троек, написанная обычным двенадцатым шрифтом, протянется примерно до Марса. Обращаю внимание, что это не число длиной от Земли до Марса, это башня степеней такой высоты.

Пять троек в этой башне покрывают гуголплекс, вычисление первого дециметра троек сжигает все предохранители компьютеров планеты, а остальные миллионы километров степеней уже как бы и ни к чему, они просто в открытую насмехаются над читателем, считать их бесполезно.

Переходим к четырем стрелочкам. Тут просто приведу картинку, раскрывающую схему вычисления четырех стрелочек, когда каждое следующее число башни степеней определяет высоту башни степеней, определяющую высоту башни степеней, определяющую высоту башни степеней… и так до самозабвения.

Рассчитывать его бесполезно, да и не получится. Количество степеней здесь не поддается осмысленному учету. Это число невозможно представить, его невозможно описать. Можно говорить, что оно огромно, что грандиозно, что монументально и заглядывает за горизонт событий. То есть придать ему какие-то словесные эпитеты. Но визуализация, даже вольная и образная — невозможна. Если с тремя стрелочками еще хоть что-то удавалось сказать, нарисовать башню от Земли до Марса, как-то с чем-то сопоставить, то тут аналогий быть просто не может. Попробуйте вообразить себе тонкую башню из троек от Земли до Марса, рядом еще одну почти такую же и еще одну, и еще… Бескрайнее поле башен уходит вдаль, в бесконечность, башни повсюду, башни везде. И, что самое обидное, эти башни даже отношения к числу не имеют, они лишь определяют высоту других башен, которые нужно построить, чтобы получить высоту башен, чтобы получить высоту башен… чтобы через невообразимое количество времени и повторений получить само число.

Вот, что такое q 1, вот что такое 3↑↑↑↑3.

Теперь от q 1, с новыми силами возвращаемся к штурму числа Грэма. Заметили, как нарастает эскалация от стрелочки к стрелочке?

3↑3 = 27

3↑↑3 = 7 625 597 484 987

3↑↑↑3 = башня, высотой от Земли до Марса.

3↑↑↑↑3 = число, которое невозможно ни представить, ни описать.

А вообразите какой цифровой кошмар творится, когда стрелок окажется пять?

Когда их шесть? Можете представить число, когда стрелок будет сто? Если можете, позвольте предложить вашему вниманию число q 2. в котором количество этих стрелок оказывается равно q 1, то есть = 3↑↑↑↑3.

Все, что было написано до сих пор, все эти расчеты, степени и башни не помещающиеся в мультивселенные мультивселенных нужны были только для одного. Чтобы показать КОЛИЧЕСТВО СТРЕЛОК в числе q 2!!!