Антонио Лизана - Если бы числа могли говорить. Гаусс. Теория чисел

3. Можно провести любую окружность с центром в любой точке и с любым радиусом.

4. Все прямые углы подобны, то есть имеют одинаковый размер и совпадают, если их наложить друг на друга перемещением.

5. Через точку, не принадлежащую прямой, можно провести единственную прямую, параллельную данной.

На самом деле, Евклид должен был бы включить еще два постулата, которыми он пользуется в своих доказательствах:

— две окружности, центры которых разделены расстоянием меньше суммы радиусов, пересекаются в двух точках (Евклид пользуется им в своем первом построении);

— два треугольника с двумя равными сторонами и равными соответственными углами подобны, то есть имеют равные углы и стороны и, следовательно, имеют одну и ту же форму и размер.

Евклид (325-265 до н.э.) — греческий математик и геометр, известный как отец геометрии. О его жизни мы знаем крайне мало, кроме того, что он жил в Александрии во время правления Птолемея I. Его работа «Начала» — одна из самых известных научных работ в мире и, после Библии, наиболее часто издаваемая и переводимая. В нее входят сведения, которые Евклид распространял в Александрийской библиотеке, и это все геометрическое знание того времени. В «Началах» в строгом виде, на основе исключительно пяти постулатов, рассказывается о свойствах линий и плоскостей, кругов и сфер, треугольников и конусов, и так далее, то есть правильных форм. Возможно, ни один из результатов в «Началах» не был впервые доказан Евклидом, но именно он организовал материал и систематизированно изложил его. Самые известные доказательства Евклида соответствуют следующим теоремам:

— сумма внутренних углов любого треугольника равна 180°;

— в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов (знаменитая теорема Пифагора).

Страница «Начал» Евклида из так называемого Манускрипта d’Orville, написанного на греческом языке в Константинополе в 888 году, который хранится в Бодлианской библиотеке Оксфордского университета.

Евклидова геометрия не только стала мощным инструментом дедуктивного рассуждения, но и оказалась чрезвычайно полезной во многих отраслях знания, например в физике, астрономии, химии и инженерных областях. В работу Евклида изменения не вносились вплоть до XIX века, пока Гаусс не сформулировал несколько видов неевклидовой геометрии, исключив ее пятый постулат.

Евклид предположил, что все постулаты очевидны и не требуют доказательства. Это не подвергалось сомнению до такой степени, что Кант в своей «Критике чистого разума» утверждал: понятия Евклида являются существенным компонентом нашего видения мира. Однако оказалось, что последний постулат в некотором роде независим и что можно отрицать его, не войдя в противоречие с предыдущими. Идея в том, чтобы по-новому определить параллельные линии, перенеся это понятие в иные, отличные от плоскости, пространства.

Начиная с 1813 года Гаусс разрабатывал геометрию, в которой отрицался последний постулат Евклида. Ученый при этом развивал идеи, которые появились у него в последние годы обучения в Коллегии Карла в разговорах с Вольфгангом Бойяи. В 1816 году Гаусс сообщил эти идеи в письме Шумахеру, своему другу и преподавателю астрономии, но, как всегда, ничего не опубликовал на эту тему. Впрочем, причиной на этот раз могло быть не только желание найти как можно более точное доказательство. Все, что касалось обсуждения постулатов Евклида, стало бы объектом ожесточенных споров, а Гауссу не нравилось участвовать в дискуссиях такого рода, которые казались ему скорее философскими.

Когда в 1831 году Янош Бойяи (1802-1860), сын Вольфганга, изложил ему свои идеи о неевклидовой геометрии, Гаусс ответил ему так: «Я не могу хвалить Вашу работу, поскольку, сделав это, я бы хвалил самого себя, так как идеи, которые Вы мне излагаете, совпадают с идеями, которые я разработал 30-35 лет назад». Однако Гаусс признал Яноша Бойяи и Николая Лобачевского, другого создателя неевклидовой геометрии, гениями первой величины. Он даже выучил русский язык, чтобы иметь возможность читать работы Лобачевского в оригинале. Кроме того, математик добился, чтобы в 1842 году русского ученого признали членом Гёттингенской академии.

Сегодня Гаусса, Лобачевского и Яноша Бойяи считают создателями неевклидовой геометрии. Сейчас, помимо евклидовой, известны гиперболическая и эллиптическая геометрии, зависящие от типа кривизны (положительной или отрицательной).

Неевклидовой называется любой вид геометрии, постулаты и свойства которой отличаются от пяти постулатов Евклида.

Существует много типов неевклидовой геометрии, хотя если свести дискуссию к гомогенным пространствам, в которых кривизна пространства одна и та же в каждой точке и в которых все его точки неразличимы, можно выделить три типа геометрий:

— евклидова геометрия — удовлетворяет пяти постулатам Евклида и имеет нулевую кривизну;

— гиперболическая геометрия — удовлетворяет только первым четырем постулатам Евклида и имеет отрицательную кривизну. В этой геометрии через каждую точку, не лежащую на прямой, проходит бесконечное количество прямых, параллельных данной;

— эллиптическая геометрия — также удовлетворяет первым четырем постулатам Евклида и имеет положительную кривизну. Что касается пятого постулата Евклида, в этой геометрии через каждую точку, не лежащую на прямой, не проходит ни одной прямой, параллельной данной (вспомним, что в евклидовой геометрии проходит только одна параллельная прямая). Это случай меридианов Земли, которые в сферической геометрии (частный случай эллиптической) считаются параллельными. На рисунке изображены прямые в различных пространствах.

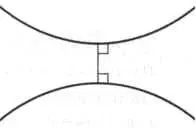
Гиперболическое пространство

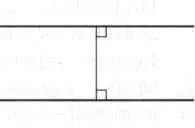
Евклидово пространство

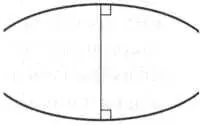
Эллиптическое пространство

В качестве примера, подтверждающего важность вклада великого немецкого математика в геометрию, можно привести тот факт, что Бернхард Риман, самый выдающийся ученик Гаусса, по его просьбе посвятил свою докторскую диссертацию обобщению неевклидовой геометрии.