Дэвид Граймс - Неразумная обезьяна [Почему мы верим в дезинформацию, теории заговора и пропаганду] [litres]

Хотя этот цинизм понятен и объясним, все же отношение к статистике как к троянскому коню, внутри которого скрывается ложь, равносильно выплескиванию вместе с водой ребенка; статистик Фредерик Мостеллер заметил по этому поводу: “Конечно, очень легко лгать с помощью статистики, но еще легче лгать без нее”. Это, несомненно, так – при правильном применении статистические инструменты трудно переоценить; статистика обнажает скрытые тренды, которые могут ускользать от внимания самых проницательных людей. Эта мощь статистических методов сделала их незаменимыми во всех сферах – от медицины до политики. Но если мы хотим получать пользу от статистики, то должны знать и о ловушках, в которые мы можем попасть при работе со статистическими данными. Особенно часто числовой информацией злоупотребляют в спорах. Нам стоит совершенствовать собственное понимание статистики, если мы не хотим пасть жертвами невежества или мошенничества.

Самое большое достижение статистики – это представление жизненных явлений в числовой, количественной форме (что, безусловно, является отличным подспорьем в нашем зыбком и неопределенном мире). Однако, к сожалению, в отсутствие адекватного контекста и понимания сути метода результаты статистических исследований могут дезориентировать и вводить в заблуждение. Для того чтобы проиллюстрировать любопытную природу статистики и вероятности, мы возьмем противоречащий интуиции пример, иллюстрирующий оба аспекта ошибок.

Представьте себе, что вы сдаете анализ на ВИЧ-инфекцию, который, как вам сказали, обладает точностью 99,99 процента. Результат анализа оказывается положительным. Какова вероятность того, что вы – носитель инфекции? Инстинкт подскажет большинству из нас, что мы почти наверняка больны, но это неверно. Правильный ответ: шанс, что у вас СПИД, равен в большинстве случаев 50 процентам. Если вас смущает этот вывод, то утешьтесь тем, что вы не одиноки. Большинство людей, в том числе профессиональные медики, приходит от такого странного утверждения в замешательство.

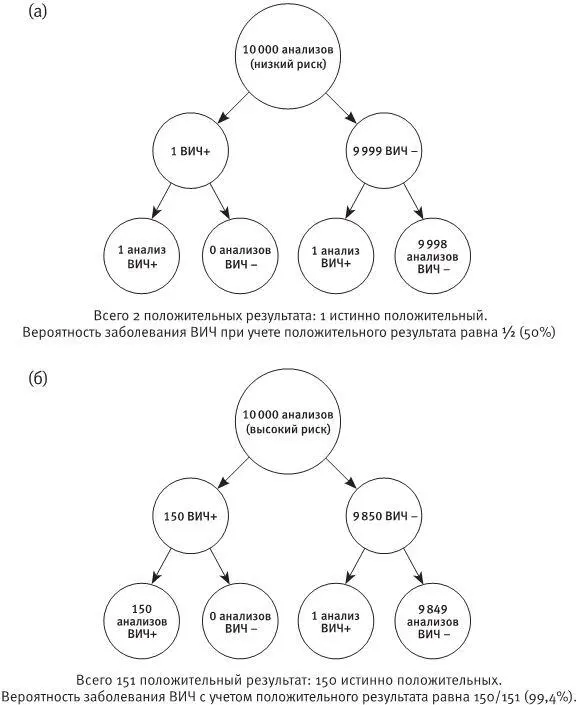
Частотное дерево, демонстрирующее надежность анализов на ВИЧ для (а) когорты низкого риска и (б) для когорты высокого риска.

Этот любопытный результат находит объяснение в теореме Байеса – математическом обосновании комбинации условных вероятностей. Теорема показывает, как ветвятся вероятности, и, в частности, сообщает нам, что вероятность заболевания ВИЧ при получении положительного результата анализа зависит не только от этого результата, но и от того, насколько в целом велика вероятность заболеть ВИЧ. Несмотря на то, что сам анализ почти совершенен, его точность зависит от другого условия, а именно – от априорной вероятности того, что у пациента вообще есть вирус. Мы не станем углубляться в формальное доказательство теоремы Байеса, так как это выходит за рамки настоящей книги и лишь напугает тех, кто незнаком с математическими символами. Однако логику теоремы понять легко, как легко и ее проиллюстрировать, несмотря на то, что истина прячется за парадоксально выглядящими статистическими выкладками.

Вернемся, однако, к нашему примеру. Каким образом тест с чувствительностью 99,99 процента может показать, что у человека с положительным результатом вероятность заболевания равна всего 50 процентам? Для человека из группы низкого риска вероятность заболеть СПИДом равна приблизительно 1:10 000. Теперь представьте себе, что 10 000 человек из этой группы низкого риска приходят сдавать анализ на ВИЧ. Один из них носитель ВИЧ, и результат его анализа практически наверняка окажется положительным. Но среди оставшихся, в связи с малой неточностью теста, один результат окажется ложноположительным. Таким образом, мы получим два положительных результата, лишь один из которых будет истинно положительным, – а это означает, что у пациента с положительным результатом вероятность заболевания равна именно 50 процентам.

Важно понимать, что такой удивительный результат не говорит о неадекватности самого анализа: в нашем примере тест отличается невероятной точностью. Главное заключается в том, что вследствие малой заболеваемости условная вероятность намного ниже той, какую мы ожидаем. На самом деле априорная вероятность того, что данный конкретный пациент инфицирован, неразрывно связана с достоверностью результата. Предположим, что тот же анализ делают людям из когорты высокого риска, например наркоманам, вводящим себе внутривенно героин. Частота инфицированности в этой группе равна приблизительно 1,5 процента. Снова представим себе, что анализ сдают 10 000 таких пациентов. В этой когорте у 150 человек тест окажется положительным ввиду истинной инфицированности. Из оставшихся 9 850 пациентов приблизительно у одного результат будет ложноположительным. Вероятность заражения при положительном результате в этой группе уже не равна 50/50 – в данном случае вероятность будет равна 150/151 или 99,34 процента, то есть намного больше, чем у пациента из когорты низкого риска.

Сценарии для случаев низкого и высокого риска можно для наглядности представить в виде частотного дерева, изображенного на рисунке. Разница между этими сценариями весьма велика, и на ней надо остановиться подробнее. Мы имеем полное право спросить: зачем нужна такая стратификация? Почему в одной группе тест дает вероятность, разительно отличающуюся от вероятности в результате того же теста в другой группе? Инстинктивно мы чувствуем, что здесь что-то не так, но мы ошибаемся: тест одинаков в обоих случаях, и его точность не может избирательно улучшаться или ухудшаться в зависимости от принадлежности пациента к той или иной группе. Реактивы не обладают ясновидением, и чувствительность теста остается равной 99,99 процента для любого пациента. Главное заключается в следующем: теорема Байеса показывает, что одной голой информации о результате недостаточно для правильного вывода – последний всегда зависит от других вероятностей. Вероятности часто оказываются условными, и голые численные данные, лишенные контекста, подлежат тщательному анализу.

Все это служит иллюстрацией того факта, что, несмотря на кажущуюся интуитивную природу вероятности и статистики, их мнимая простота скрывает многослойную сложность, которую легко упустить из виду. В итоге мы можем сделать абсолютно ошибочные выводы, а сомнительные выводы и неверная интерпретация статистических данных часто имеют катастрофические последствия. Рассуждения, приводящие к неверным заключениям, любопытны не только своей бессодержательностью с точки зрения науки или тем, что демонстрируют “математическую ловкость рук”: мы живем в эпоху, когда статистическая информация служит основой принятия решений во всех вообразимых сферах деятельности – от науки до политики, экономики и всего, что располагается между ними. Такое повсеместное проникновение статистики и вероятности в нашу действительность означает, что они часто причастны к вопросам жизни и смерти, будь то лечение болезней или работа правительства.