Дэвид Граймс - Неразумная обезьяна [Почему мы верим в дезинформацию, теории заговора и пропаганду] [litres]

Этот странный вопрос был несколько видоизмененным заданием, которое получали участники телевизионного шоу Let’s Make a Deal , когда ведущий Монти Холл ставил их перед подобным выбором – сменить решение или остаться при своем мнении. Действительно, если остаются две двери, то шансы угадать дверь с автомобилем составляют 50 на 50, и разве это важно – изменит свое мнение участник или нет? Но Савант дала иной ответ. Она ответила, что самая выгодная тактика – сменить дверь. Редакцию захлестнул поток яростных писем, авторы которых уличали Мэрилин в невежестве. Из более чем 10 тысяч писем приблизительно 1000 были написаны людьми с докторской степенью, в том числе математиками и другими учеными. В этих письмах Мэрилин сурово укоряли за пропаганду математического невежества.

Но вос Савант была права: смена двери после того, как ведущий открыл одну из них, действительно повышает шанс участника на выигрыш до 2/3; если же участник останется при своем первоначальном мнении, то шансы выиграть уменьшатся до 1/3. Дай себе критики вос Савант труд разобраться в вопросе глубже, они узнали бы, что эту “проблему Монти Холла” поставил и решил в 1975 году статистик Стив Селвин. Но каким образом может быть верным такой странный ответ? Представим себе, что автомобиль находится за дверью A. Если вы первоначально выбрали эту дверь, то Монти обнаружил бы козу за дверью B или C. Если вы измените свое решение, то проиграете. Но представим себе, что вы сначала выбрали дверь B: Монти откроет дверь C, и если вы измените свое решение, то выиграете. Точно так же, если вы выберете дверь C, то открыта будет дверь B, и изменение решения снова принесет вам выигрыш. То есть в двух третях случаев изменение стратегии становится выигрышным.

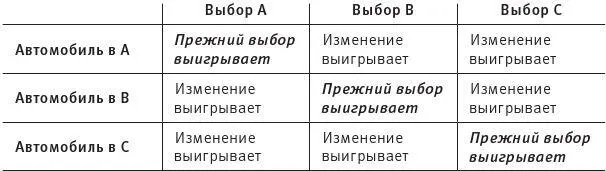
В представленной матрице выигрышей представлены все возможные случаи, и в двух третях их изменение первоначального выбора приводит к выигрышу. Это выглядит абсурдным, потому что интуитивно мы чувствуем, что изменение выбора не играет в вероятности выигрыша никакой роли. Если вы считаете результат озадачивающим, то не переживайте: вы оказались в хорошей компании. Как и авторы гневных писем в журнал Parade , известный математик Пал Эрдёш тоже долго сомневался в истинности решения вос Савант – до тех пор, пока его не убедила компьютерная имитация решения проблемы Холла. Сегодня проблема Монти Холла приводится как хрестоматийная в учебниках по теории вероятностей, но тем не менее, как мы видим, продолжает сбивать с толку в том числе и специалистов. Поразительно, но эксперименты с голубями показывают, что даже эти птицы быстро усваивают стратегию изменения выбора, находя ее оптимальной. Поведение птиц являет собой разительный контраст с поведением людей, по поводу чего экспериментаторы сухо отметили: “Повторение процедуры с участием людей показало, что люди не принимают оптимальной стратегии даже при интенсивном обучении”.

Наша врожденная способность искать и находить закономерности во всем, с чем мы сталкиваемся, является одной из важнейших для выживания вида способностей. Стремление придать смысл окружающему нас миру и ненасытное любопытство привели нас к созданию цивилизации, великим открытиям и покорению физического мира. Но этот тонкий инстинкт может полностью отказать нам в помощи, когда в повседневной жизни мы сталкиваемся с шумными и хаотичными нагромождениями разнородных элементов. В мире неопределенностей теория вероятностей и статистика, если ими мудро пользоваться, позволяют, подобно острому лезвию, отсекать реальность от иллюзий. Случайные события можно понимать как вероятности, как область, фундаментально важную для всех видов деятельности, – начиная с планирования городов и квантовой механики и заканчивая медицинскими и экономическими исследованиями. Несмотря на использование статистики в таких сложных областях, зарождение этих методов имело место из-за весьма приземленной мотивации, а именно – из-за стремления выигрывать в азартные игры. Человечество увлекается ими тысячи лет, но вплоть до семнадцатого века капризы игры в кости считались выходящими за рамки человеческого понимания; неисповедимые пути удачи целиком зависели от воли богов. Сама идея о том, что исход можно предсказать с определенной степенью точности, казалась безумной и даже святотатственной.

Возможно, так бы оно все и осталось, если бы вопрос, заданный в 1664 году эксцентричным французским писателем шевалье де Мере, не заинтриговал величайших интеллектуалов Франции семнадцатого века – Блеза Паскаля и Пьера де Ферма. Паскаль в конечном счете разрешил проблему де Мере, доказав, что выпадение одной шестерки при четырех бросках одной кости немного более вероятно (51,77 процента), чем выпадение по крайней мере одной пары шестерок при 24 бросках двух костей (49,14 процента). Великие умы предреволюционной Франции тратили свои недюжинные способности на подсчет шансов обогащения, которого так жаждали завзятые игроки. Исследование игры в кости привело к рождению теории вероятностей, возникшей, таким образом, благодаря непритязательной салонной игре. Но, как мы уже видели, наше восприятие настроено на поиск закономерностей, а следовательно, мы склонны неверно трактовать стохастические, или случайные, события. По-настоящему случайные события не обладают “памятью” о предыдущих исходах, однако человеческая склонность к экстраполяции результатов наблюдений часто приводит нас к ошибочным выводам.

Возьмем для примера лотерею. Если она проводится честно, то выпадение чисел 1, 2, 3, 4, 5 и 6 настолько же вероятно, как и выпадение любой другой комбинации. Тем не менее интуитивно мы считаем такую последовательность маловероятной и избегаем ее. Точно так же, если при честном бросании монеты двадцать раз подряд выпадает решка, то мы надеемся, что уж на двадцать первый раз “точно” выпадет орел, несмотря на то, что вероятность все равно остается равной 50 процентам [52]. Это убеждение называют ошибкой игрока , и она часто доводила людей до разорения. Но, слава всевышнему, мы не полностью отдаем себя на милость инстинкта – полезного, но порой и вводящего в заблуждение: человеческая любознательность за прошедшие века привела нас к созданию инструментов, позволяющих отличать шум от полезного сигнала.

В двадцать первом веке статистическая и вероятностная информация пропитала все поры общественной жизни – от маркетинга и медицины до результатов спортивных состязаний и прогнозов погоды. Статистика сохраняет свою привлекательность благодаря своей кажущейся интуитивности. Но этот флер простоты часто оказывается обманчивым, скрывающим тонкости, которые могут опровергнуть все наши выводы и расстроить наши планы. Непрозрачность статистики и широко распространенная математическая безграмотность позволяют многим несведущим людям неверно интерпретировать статистические тренды. Хуже того: эти же два обстоятельства предоставляют мошенникам и темным дельцам возможность манипулировать нами, используя статистику для подтверждения ложных аргументов. Подобные манипуляции вредят нам как сообществу, и циничное отношение к статистике вызывает у нас вполне объяснимую симпатию; недаром такой популярностью пользуется саркастическое замечание о трех степенях нечестности: “ложь, наглая ложь и статистика”, которое приписывают множеству великих остроумцев – от Оскара Уайльда до Марка Твена.