Наталия Пылаева - Преодоление трудностей учения: нейропсихологический подход

Поскольку достаточной интериоризации программы не произошло и в следующем задании, детям была предложена специальная работа на дополнение программы (задание «Черепаха»). Каждый ребенок получил рисунок черепахи с пронумерованными пятнами панциря и с двумя рядами цифр: красного и зеленого цвета.

Детям был задан вопрос: «Как вы думаете, как надо закрашивать черепаху?».

Ответ: «Нужно раскрасить ее двумя цветами, как указано в задании: 15, 13, 11 – красным, а 14, 12, 10 – зеленым». Вопрос: «А какие еще пятна нужно закрасить красным цветом?».

Дети не смогли ответить на этот вопрос. Вопрос: «Как можно продолжить ряд 15, 13, 11?». Дети вновь не смогли найти ответ.

Педагог: «Здесь нужно считать через один. Какая цифра будет следующей?».

Дети хором (кроме учениц Б и Г): «9, 7, 5…».

В процессе пересчета ученик Е сбился, перейдя на полный

прямой ряд: «5, 6, 7».

Педагог предложил дописать ряд, то есть достроить первую программу.

Все дети (кроме ученицы Б) сделали это без ошибок, одни самостоятельно, а другие при организующей помощи. Дописывание четного ряда выполнялось самостоятельно, и здесь дети допустили больше ошибок как из-за неупроченности дискретного ряда, так и из-за трудностей переключения. Графическая реализация программ была успешной.

По-видимому, начинать работу с неполными и дискретными рядами целесообразно с повторения материала упроченных ситуаций и отработки действия в материализованной форме: этажи, лифт, четная и нечетная стороны улиц; раскладывание дискретного обратного ряда должно предшествовать дополнению программ или составлению программ по аналогии. Более широко может использоваться четный и нечетный неполный ряды. Тем не менее усвоение четного и нечетного рядов не должно быть самоцелью, главное – возможность действия по программе.

Параллельные ряды.Последний цикл был проведен на наиболее сложном материале – параллельных рядах, требующих большего распределения внимания и, соответственно, большей опоры на программу.

Задания с параллельными рядами предполагают одновременное выполнение двух подпрограмм. Они могут быть:

а) идентичными (два ряда цифр в прямом или обратном порядке);

б) аналогичными (прямой порядок букв и цифр по алфавиту);

в) разнонаправленными (один ряд в прямом порядке, второй – в обратном).

В описываемом курсе занятий дети выполнили 7 заданий первых двух типов.

Как всегда, новый тип заданий вводился в наиболее развернутом виде с опорой на материализованную форму программы и ее реализацию.

В первом задании ребенку предлагалась таблица с цифрами двух цветов от 1 до 10 и два набора карточек с цифрами соответствующих цветов. Работа начиналась с раскладывания по порядку ряда цифр сначала одного цвета, а под ним – другого. Все дети справились с этим безошибочно. Далее педагог показал порядок выполнения программы (1–1 – 2–2) и предложил «прочитать» программу целиком, что дети сделали без затруднений. После этого успешного пробного действия было задание складывать карточки в таблицу таким же образом. Дети в основном успешно следовали программе, но иногда соскальзывали на другой цвет, беря цифру нижнего ряда вместо верхнего. Далее дети должны были вернуть цифры на место, следуя той же программе, но уже не представленной во внешнем плане. Возвращая цифры, дети соблюдали порядок от 1 до 10, но допускали соскальзывание на другой цвет чаще, чем в предыдущем варианте задания.

К третьему заданию, которое состояло из параллельного обведения цифр в двух таблицах и их последующего показа, программа действия была достаточно интериоризована, что позволило детям безошибочно показать цифры при отсутствии образца.

Однако оперирование параллельными рядами с обратным порядком было успешным лишь у части детей. Так, ученица Д, работая с обратным порядком в первый раз, справилась с заданием за 68 с, допустив ошибку соскальзывания на другой цвет, несмотря на наличие наглядной программы. В дальнейшем, действуя без образца, девочка в аналогичном задании успешно осуществила поиск за 55 с. Ученица Г., в целом усвоив программу к последнему заданию, тем не менее допустила в нем ошибку следования программе.

Итак, в ходе выполнения этого цикла, как и предыдущих четырех, была обнаружена положительная динамика возможностей детей к действию по программе. Они стали меньше действовать методом проб и ошибок, этап ориентировки в задании стал для них более обязательным. Теперь они более последовательно реализовывали программу и лучше контролировали свои действия. При этом развилась возможность интериоризации программ, даже таких сложных, как в заданиях с параллельными рядами. Одновременно автоматизировался счет в прямом и обратном порядке. Кроме того, разносторонняя работа с цифрами привела к упрочению зрительного образа цифр, исчезновению ошибок типа зеркальности, улучшению графических навыков.

Проиллюстрируем динамику возможностей детей к программированию и контролю своих действий на примерах выполнения заданий учениками А и Е, имевшими в начале коррекционного курса наибольшие трудности в этом отношении (рис. 2.2.1).

Рис. 2.1.1.Выполнение заданий ученицей А: 1 – рисунок по точкам (цикл 2); 2 – «Буратино» (цикл 4); 3 – «Черепаха» (цикл 4)

Напомним, что именно эти дети «не взяли» программу в контрольном задании на шифровку «цифры – точки»: ученица А, игнорируя программу, стала ставить по одной точке в каждую ячейку, а ученик Е инертно воспроизводил нарастающее количество точек от 1 до 4, как в образце, не ориентируясь на цифры в верхней строке таблицы (рис. 2.2.2).

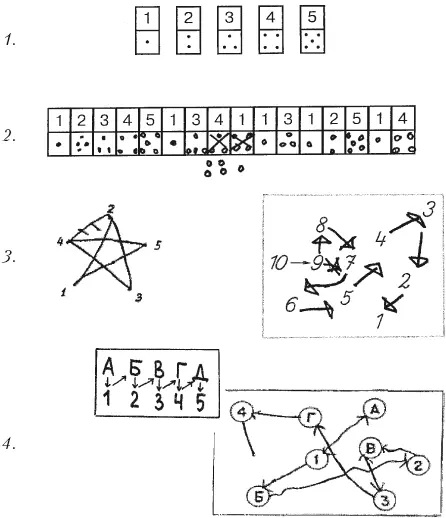
Рис. 2.2.2.Выполнение заданий учеником Е: 1 – контрольное задание шифровки «цифры – точки»; 2 – рисунок по точкам (цикл 2); 3 —«по маршруту» (цикл 4); 4 – «по маршруту» (цикл 5)

Как показывают образцы выполнения заданий этими детьми, в начале коррекционного курса они допускали ошибки даже в элементарных заданиях на рисование по пронумерованным точкам (см. рис. 2.2.1, 1) и 2.2.2, 2). В середине цикла ученики допускали ошибки уже в более сложных заданиях. Так, ученица А в задании «Буратино» (см. рис. 2.2.1, 2), правильно найдя ошибку в программе, построенной Буратино, при самостоятельном написании программы обратного ряда сделала две ошибки: сначала начала писать прямой ряд, затем пропустила цифру 6. Ученик Е в задании на обратный ряд пропустил цифру 8 (см. рис. 2.2.2, 3). К концу же цикла для детей стало возможным выполнение весьма трудных заданий, как, например, на дискретный обратный ряд (ученица А) (см. рис. 2.2.1, 3) и на параллельные ряды (ученик Е) (см. рис. 2.2.2, 4). Для оценки эффективности коррекционного курса, кроме анализа текущей динамики, использовались данные контрольных срезов.