Капра Фритьоф - Паутина жизни. Новое научное понимание живых систем

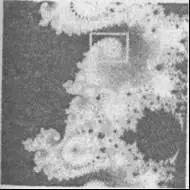
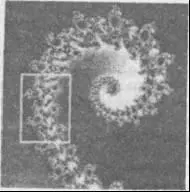
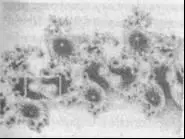
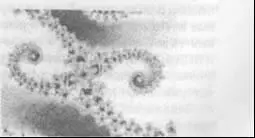
Рис. 6-20.

Стадии путешествия вглубь множества Мандельбро. На каждой фотографии область последующего увеличения помечена белой рамкой.

Из PeitgenandRichter (1986)

На каждой стадии изменения масштаба этого фантастического путешествия — в ходе которого мощности сегодняшних компьютеров обеспечивают 100 000 000-кратное увеличение! — картина напоминает причудливо изрезанное побережье; образы, изобилующие в узорах этого «побережья», удивительно напоминают органические существа во всей их бесконечной сложности. И на каждом шагу нас ждет головокружительное открытие: мы снова и снова обнаруживаем мельчайшую копию всего множества Мандельбро, глубоко запрятанную в структуре его границы.

Как только изображение множества Мандельбро появилось в августе 1985 года на обложке «ScientificAmerican», сотни компьютерных энтузиастов принялись использовать итеративную программу, опубликованную в этом номере, для собственных путешествий на домашних компьютерах в дебри множества. Паттерны, обнаруженные в этих путешествиях, эффектно раскрашивались, а полученные картины публиковались в многочисленных книгах и показывались на выставках компьютерного искусства во всех уголках мира37. Рассматривая эти изумительно красивые изображения закрученных спиралей, водоворотов, морских коньков, органических форм, расцветающих и превращающихся в пыль, нельзя не заметить поразительного сходства этих картин с психоделическим искусством 1960-х годов. Это было искусство, инспирированное схожими путешествиями, но содействовали им не компьютеры и новая математика, а ЛСД и другие психоделические наркотики.

Термин психоделический («проявляющий разум») был изобретен не случайно: подробные исследования показали, что эти наркотики действуют на человека как усилители, или катализаторы, его собственных психических процессов38. Можно предположить поэтому, что фрактальные паттерны, столь поразительно проявляющиеся в ЛСД-опыте, каким-то образом встроены в человеческий мозг. Фрактальная геометрия и ЛСД были открыты почти одновременно: это еще одно из тех невероятных совпадений — или синхронизмов? — которые часто происходят в истории идей.

Множество Мандельбро можно рассматривать как склад, резервуар паттернов с их бесконечными деталями и вариациями. Строго говоря, оно не самоподобно, поскольку не только снова и снова повторяет одни и те же паттерны, включая маленькие копии всего множества, но и содержит, кроме этого, элементы из бесконечного набора множеств Жулиа! Таким образом, это сверхфрактал непостижимой сложности.

И вместе с тем эта структура, превосходящая своей сложностью все пределы человеческого воображения, строится на основе нескольких очень простых правил. Другими словами, фрактальная геометрия, как и теория хаоса, вынудила ученых и математиков пересмотреть само понятие сложности. В классической математике простые формулы соответствуют простым формам, сложные формулы — сложным формам. В новой математике сложных систем ситуация радикально другая. Простые уравнения могут генерировать поразительно сложные странные аттракторы, а простые правила итерации порождают структуры более сложные, чем мы можем себе представить. Мандельбро видит в этом новое волнующее направление в науке:

Это очень оптимистичный результат, потому что в конце концов изначальный смысл изучения хаоса состоял в попытке найти простые законы в окружающей нас Вселенной… Человек всегда направляет свои усилия на поиск простых объяснений для сложных реальностей. Однако контраст между простотой и сложностью никогда еще не был сравним с тем, что мы находим здесь39.

Огромный интерес к фрактальной геометрии распространился далеко за пределы математического сообщества. Мандельбро видит в этом здоровое направление развития общества. Он надеется, что это положит конец изоляции математики от других видов человеческой деятельности и повсеместному игнорированию математического языка даже среди людей, в общем, высокообразованных.

Эта изоляция математики — поразительный показатель нашей интеллектуальной разобщенности, и в этом смысле она относительно нова. На протяжении нескольких веков многие великие математики вносили выдающийся вклад и в другие области. Так, в XI веке, персидский поэт Омар Хайям, всемирно известный автор «Рубапят», написал, помимо этого, новаторскую книгу по алгебре и служил официальным астрономом при дворе халифа. Декарт, основатель современной философии, был блестящим математиком, а также практиковал медицину. Оба изобретателя дифференциального исчисления, Ньютон и Лейбниц, проявляли активность и в других областях знания помимо математики. Ньютон был натурфилософом и внес фундаментальный вклад практически во все разделы науки, известные в его времена, а кроме того, в алхимию, теологию и историю. Лейбниц известен прежде всего как философ, но он также был основателем символической логики и большую часть своей жизни вел активную деятельность в качестве дипломата и историка. Великий математик Гаусс был также физиком и астрономом, изобрел несколько полезных технических устройств, в том числе электрический телеграф.

Эти примеры, к которым можно добавить не один десяток других, показывают, что на протяжении всей нашей интеллектуальной истории математика никогда не была изолирована от других сфер человеческого знания и деятельности. В XX веке, однако, прогрессирующий редукционизм, фрагментация и специализация привели к крайней степени изоляции математики даже внутри научного сообщества. Так, теоретик хаоса Ральф Эбрем вспоминает:

Когда я начал свою профессиональную деятельность в математике в 1960 году, то есть не так уж давно, математика во всей ее полноте отвергалась физиками, включая и самых авангардных математических физиков… Было отвергнуто все, что еще год или два назад использовал Эйнштейн… Физики отказывали старшекурсникам в разрешении на посещение математических курсов, проводимых математиками: «Учитесь математике у нас. Мы научим вас тому, что вам следует знать»… Это было в 1960 году. К 1968 году ситуация изменилась полностью40.

Великое очарование теорией хаоса и фрактальной геометрией, распространившееся среди людей, которые работают в разных областях — от ученых до менеджеров и художников, — возможно, и в самом деле свидетельствует, что изоляции математики приходит конец. В наше время новая математика сложных систем все чаще побуждает людей к осознанию того, что математика вообще — это нечто намного большее, чем сухие формулы; что понимание паттерна — необходимый путь к пониманию окружающего нас живого мира; и что все проблемы паттерна, порядка и сложности — это проблемы существенно математического характера.