Капра Фритьоф - Паутина жизни. Новое научное понимание живых систем

Комплексные числа

Вершиной фрактальной геометрии стало открытие Мандельбро математической структуры, которая обладает ошеломляющей сложностью и все же может быть воспроизведена с помощью очень простой итеративной процедуры. Чтобы понять эту поразительную фрактальную фигуру, известную как множество Мандельбро, необходимо сначала ознакомиться с одним из важнейших математических понятий — комплексными числами.

Открытие комплексных чисел стало восхитительной главой в истории математики28. Когда в средние века возникла алгебра и математики принялись исследовать все виды уравнений и классифицировать их решения, они вскоре столкнулись с задачами, не имевшими решения в рамках множества известных им чисел. В частности, уравнения типа х + 5 = 3 заставили их расширить понятие числа до отрицательных чисел, так чтобы решение могло быть записано как х = -2. В дальнейшем так называемые действительные числа — положительные и отрицательные целые числа, дроби и иррациональные числа (например, квадратные корни или знаменитое число п) — стали представлять как точки на единой плотно населенной числовой оси (рис. 6-16).

— 5/2 1/2 π

— 4–3 -2 -1 0 1 2 3 4

Рис. 6-16 Числовая ось

С таким расширением понятия числа все алгебраические уравнения, в принципе, могли быть решены — за исключением тех, где фигурировали квадратные корни отрицательных чисел. Уравнение х2 = 4 имеет два решения: х = 2 и х = -2; однако для х2 = -4, по всей видимости, не должно быть решения, поскольку ни +2, ни — 2 при возведении в квадрат не дадут -4.

Древние индийские и арабские алгебраисты постоянно встречались с такими уравнениями, но отказывались даже записывать выражения типа, считая их абсолютно бессмысленными. И только в XVI веке квадратные корни отрицательных чисел стали появляться в алгебраических текстах, но и тогда авторы спешили пояснить, что такие выражения на самом деле ничего не означают.

Декарт называл квадратный корень отрицательного числа «мнимым числом» и был уверен, что появление таких мнимых чисел в расчетах означает, что проблема неразрешима. Другие математики использовали термины «фиктивные», «фальшивые» или «невозможные» для обозначения величин, которые сегодня мы, с легкой руки Декарта, все еще называем мнимыми числами.

Поскольку квадратный корень отрицательного числа не может быть помещен ни в одной точке числовой оси, математики, вплоть до XIX столетия, не могли наделить эти величины никаким реальным смыслом. Великий Лейбниц, изобретатель дифференциального исчисления, приписывал выражению мистические свойства, видя в нем проявление Божественного Духа и называя его «этой амфибией между бытием и небытием»29. Столетие спустя Леонард Эйлер, самый плодотворный математик всех времен, выразил ту же мысль в своей «Алгебре» словами хотя и менее поэтичными, но все же содержащими отголосок Чуда:

Следовательно, все такие выражения, как, и т. п., есть невозможные, или мнимые числа, поскольку представляют корни отрицательных величин; по поводу таких чисел мы можем достоверно утверждать, что они ни ничто, ни нечто большее, чем ничто, ни нечто меньшее, чем ничто, из чего неизбежно следует, что они мнимы, или невозможны30.

В XIX веке другой математический гений, Карл Фридрих Гаусс, окончательно и твердо провозгласил, что «этим мнимым сущностям может быть приписано объективное бытие»31. Гаусс, конечно, понимал, что мнимым числам не найдется места на числовой оси, а поэтому он попросту поместил их на перпендикулярную ось, которую провел через нулевую точку основной оси, построив таким образом декартову систему координат. В этой системе все действительные числа располагаются на действительной оси, а все мнимые числа — на мнимой оси (рис. 6-17 называется мнимой единицей и обозначается символом i. А поскольку любой квадратный корень отрицательного числа всегда может быть представлен как = = i , то все мнимые числа можно расположить на мнимой оси как кратные»'.

Таким остроумным способом Гаусс создал прибежище не только для мнимых чисел, но и для всех возможных комбинаций действительных и мнимых чисел, например, (2 + i), (3 — i) и т. п. Такие комбинации получили название комплексных чисел; они представлены точками на плоскости, которая называется комплексной плоскостью и образована действительной и мнимой осями. В общем случае любое комплексное число можно записать в виде

z = х + iy,

где х — действительная часть, а у — мнимая часть.

Введя это определение, Гаусс создал специальную алгебру комплексных чисел и разработал множество фундаментальных идей в области функций комплексного переменного. В конце концов это привело к появлению целого раздела математики, известного как комплексный анализ, который выделяется огромным диапазоном применений в самых разнообразных областях науки.

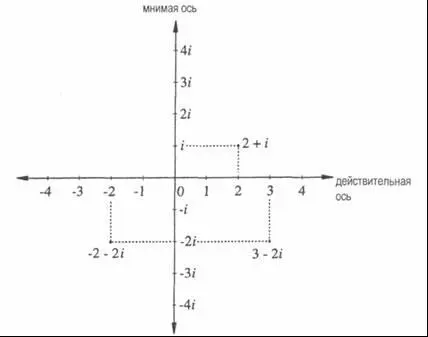
Рис. 6-17. Комплексная плоскость

Паттерны внутри паттернов

Причина, по которой мы затеяли этот экскурс в историю комплексных чисел, заключается в том, что многие фрактальные формы могут быть воспроизведены математически, с помощью итеративных процедур на комплексной плоскости. В конце 70-х годов, опубликовав свою новаторскую книгу, Мандельбро обратил внимание на особый класс математических фракталов, известных как множества Жулиа32. Эти множества были открыты французским математиком Гастоном Жулиа в начале XX столетия, но скоро канули в безвестность. Интересно отметить, что Мандельбро впервые наткнулся на работы Жулиа еще студентом, посмотрел на его примитивные рисунки (выполненные в те времена без помощи компьютера) и потерял к ним интерес. Спустя полвека, однако, Мандельбро понял, что рисунки Жулиа представляют собой грубые наброски сложных фрактальных форм; и он принялся подробно воспроизводить их с помощью самых мощных компьютеров, какие только сумел найти. Результаты оказались поразительными.

В основу множества Жулиа положено простое отображение

Z→ Z2 + С,

Где z — комплексная переменная, а с — комплексная постоянная. Итеративная процедура состоит в выборе любого числа z на комплексной плоскости, возведении его в квадрат, добавлении константы с, возведении результата в квадрат, добавлении к нему константы с и т. п. Когда это вычисление выполняется с различными начальными значениями z, некоторые из них будут увеличиваться до бесконечности в ходе процесса итерации, в то время как другие остаются конечными33. Множество Жулиа — это набор всех тех значений z, или точек на комплексной плоскости, которые при итерации ограничены некоторым пределом, т. е. конечны.