Капра Фритьоф - Паутина жизни. Новое научное понимание живых систем

И Мандельбро создал фрактальную геометрию — «язык, на котором можно говорить об облаках», — чтобы описывать и анализировать сложность нерегулярных форм в окружающем нас мире природы.

Наиболее поразительное свойство этих «фрактальных» форм заключается в том, что их характерные паттерны многократно повторяются на нисходящих уровнях так, что их части на любом уровне по форме напоминают целое. Мандельбро иллюстрирует это свойство самоподобия, отламывая кусочек цветной капусты и указывая на то, что сам по себе кусочек выглядит как маленький кочан цветной капусты25. Он продолжает демонстрацию, деля часть дальше, изымая еще один кусочек, который тоже выглядит как очень маленький кочан. Таким образом, каждая часть выглядит как целый овощ. Форма целого подобна самой себе на всех уровнях выбранного диапазона.

В природе встречается множество других примеров самоподобия. Камни в горах напоминают маленькие горы; ответвления молнии или края облаков снова и снова повторяют один и тот же паттерн; побережье моря можно делить на все более мелкие части, и в каждой из них будут проявляться подобные друг другу очертания береговой линии. Фотографии дельты реки, кроны дерева или ветвления кровеносных сосудов могут проявлять паттерны такого разительного сходства, что мы порой не можем отличить один от другого. Подобие образов совершенно различных масштабов было известно очень давно, но до Мандельбро никто не владел математическим языком для описания этого явления.

Когда в середине 70-х Мандельбро опубликовал свою новаторскую книгу, он еще сам не догадывался о связи между фрактальной геометрией и теорией хаоса, но ему и его коллегам-математикам не понадобилось много времени, чтобы обнаружить, что странные аттракторы могут служить изысканнейшими примерами фракталов. Если части их структуры увеличить, то обнаруживается многослойная субструктура, в которой вновь и вновь повторяются одни и те же паттерны. В связи с этим странные аттракторы стали определять как траектории в фазовом пространстве, в которых проявляются черты фрактальной геометрии.

Еще одна важная связь между теорией хаоса и фрактальной геометрией проявилась в переходе от количества к качеству. Как мы видели, невозможно предсказать значения переменных хаотической системы в определенный момент времени, но можно предсказать качественные особенности поведения системы. Точно так же, невозможно вычислить длину или площадь фрактальной формы, однако можно — качественным способом — определить степень ее изрезанности.

Мандельбро подчеркнул эту существенную особенность фрактальных форм, задав провоцирующий вопрос: какова протяженность побережья Британии? Он показал, что, поскольку измеряемую длину можно растягивать до бесконечности, переходя ко все более мелкому масштабу, на этот вопрос нет однозначного ответа. Зато можно определить число в диапазоне от 1 до 2, которое характеризует изрезанность побережья. Для британского побережья это число равно около 1,58; для более изрезанного норвежского берега оно близко к 1,7027.

Поскольку можно показать, что это число имеет определенные свойства размерности, Мандельбро назвал его фрактальной размерностью. Мы можем понять эту идею интуитивно, зная, что извилистая линия занимает больше пространства на плоскости, чем одномерная гладкая линия, но меньше, чем сама двухмерная плоскость. Чем больше изрезана линия, тем ближе к числу 2 ее фрактальная размерность. Подобным же образом, скомканный лист бумаги занимает больше пространства, чем плоскость, но меньше, чем сфера. Таким образом, чем плотнее скомкана бумага, тем ближе к числу 3 будет ее фрактальная размерность.

Концепция фрактальной размерности, изначально появившаяся как чисто абстрактная математическая идея, превратилась со временем в мощный инструмент анализа сложности фрактальных форм, поскольку замечательно соответствует нашему жизненному опыту. Чем более изрезаны очертания молнии или границы облаков, чем менее сглажены формы побережий или гор, тем выше их фрактальные размерности. Чтобы смоделировать фрактальные формы, встречающиеся в природе, можно сконструировать геометрические фигуры, обладающие точным самоподобием. Основным методом для построения таких математических фракталов служит итерация, т. е. многократное повторение определенной геометрической операции. Процесс итерации, который привел нас к преобразованию пекаря — математической операции, лежащей в основе странных аттракторов, — оказался, таким образом, главной математической особенностью, объединяющей теорию хаоса с фрактальной геометрией.

Одной из простейших фрактальных форм, производимых итерацией, является так называемая кривая Коха, или «кривая снежинки»27. Геометрическая операция заключается в том, чтобы разбить отрезок линии на три равные части и затем заменить центральную секцию двумя сторонами равностороннего треугольника, как показано на рис. 6-12. Повторение этой операции во все более мелких масштабах приводит к появлению кружевной снежинки (рис. 6-13). Как и в случае с изрезанной береговой линией, кривая Коха становится бесконечно длинной, если итерация продолжается бесконечно. В сущности, кривую Коха можно рассматривать как очень грубую модель береговой линии (рис. 6-14).

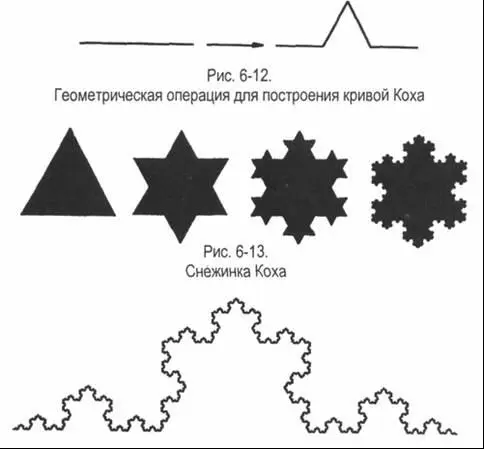
Рис. 6-14. Моделирование береговой линии с помощью кривой Коха

Математика сложных систем

С помощью компьютеров простые геометрические итерации можно применять тысячи раз в различных масштабах, производя так называемые фрактальные подделки — компьютерные модели растений, деревьев, гор, береговых линий и т. п., обладающие поразительным сходством с реальными формами, которые встречаются в природе. На рис. 6-15 приведен пример такой подделки. Производя итерацию над простым рисунком веточки в различных масштабах, удалось получить красивое и сложное изображение папоротника.

Рис. 6-15. Фрактальная подделка папоротника. Из Garcia (1991)

Этот новый математический аппарат позволил ученым строить точные модели разнообразных нерегулярных естественных форм. Занимаясь этим моделированием, они повсеместно обнаруживали присутствие фракталов. Фрактальные паттерны облаков, которые изначально воодушевили Мандельбро на поиски нового математического языка, вероятно, самые изумительные. Их самоподобие охватывает семь порядков величин, а это означает, что если границу облака увеличить в 10 000 000 раз, она будет иметь все ту же знакомую форму.