Шалва Амонашвили - Как живете, дети?

Опять обращаюсь к классу: путем мимики и жестикуляции решаем пример. Потом сразу даю знак рукой.

— 50! — произносят дети хором.

Вызванные быстро пошептались между собой, и Гоча записывает в квадратике первого примера 50 .

— Нет! — волнуются дети.

— Да! — говорят трое.

Эка внимательно смотрит на столбик и записывает ответ четвертого примера.

Так решают дети и все остальные примеры.

За сколько времени? За четыре минуты! А примеры ведь из области познавательной шалости!

Четыре минуты еще не рекорд.

— Спасибо, садитесь! — говорю я Эке, Нико, Гоче. — А теперь — три минуты поэзии!

Нато выбегает. Дети расслабляются: кто опускает голову на парту, закрывает глаза, кто полулежит — кому как удобнее.

— Сегодня я прочту грузинское народное стихотворение о том, как звери помогали старушке убирать урожай!

Нато, Ния, Тека, Ираклий, Гига умеют читать стихи вдохновенно, выразительно. Дети часто просят их прочесть стихи. Минуты поэзии на уроках математики ввели мы недавно. Эта группа детей (к ней присоединяются и другие дети) поочередно читает одно-два стихотворения, затем мы опять возвращаемся к «проблемам» математики. Сегодня очередь Нато читать стихи. Стихотворение о старушке и ее помощниках — зверях полно юмора. Нато не просто читает, она и изображает. Дети смеются и аплодируют ей.

— А завтра кто будет читать?

— Я буду читать новое стихотворение! — говорит Гига.

Открываю половину второй доски.

— За 6 минут мы должны заполнить цифрами этот квадрат и сделать его волшебным. Сначала перерисуйте его в свои тетради!

Дети выполняют.

— Эти 3 слагаемые в сумме дают...

— 15!

— Верно. В пустых квадратиках надо записать такие числа от 1 до 10, чтобы сумма слагаемых и по горизонтали ( показываю ), и по вертикали ( тоже показываю ) равнялась 15. Числа не должны повторяться. Давайте сделаем вместе! Подумаем сперва, какие числа вставить в среднюю вертикаль! Магда, не забудь посмотреть на часы, как только пройдет 5 минут, скажи!

Пробуется несколько вариантов — не получается, числа повторяются, сумма их нарушается то по одной диагонали, то по другой... Магда напоминает:

— Осталось 2 минуты... Осталась одна минута!

И на исходе последней минуты дети все же нашли правильное решение, сразу же перепроверили — верно.

От радости дети аплодируют, кричат «ура». А волшебный квадрат выглядит так:

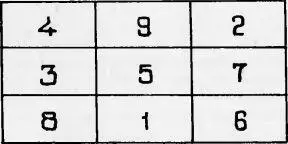
— Если кто хочет, пусть дома составит такой же волшебный квадрат, только чтобы сумма чисел была другая и, конечно, чтобы числа не повторялись!

Желание изъявляют все. «Прекрасно, дети! Вот будет головоломка сегодня и вам, и вашим близким. Зато некоторые из вас завтра придут со своими волшебными квадратиками, а некоторые будут утверждать, что волшебные квадраты больше не получаются, нужно, чтобы числа повторялись! Это мне и нужно: вы будете спорить друг с другом, доказывать, на это уйдут перемены. Вы будете учить друг друга, вот что последует за этим волшебным квадратиком и вот почему он у меня волшебный!»

За 6 минут решаются задачи о вычислении периметров треугольника с равными сторонами и прямоугольников.

— Половина стороны треугольника равна d. Чему равен периметр треугольника?

Не успел я досказать задачу, как многие уже решили ее:

— 6d. Равен 6d!

— А если d равно 3 см?

— Тогда периметр составит 18 см!

— А если d равно 4 см?

— Периметр будет 24 см!

— А если d равно двум с половиной см?

— 15!

— Ну, хорошо! Вот вам другая задача. Дано 2 равных прямоугольника, стороны которых известны. Если приставить их друг к другу равными сторонами, получится...

— Новый прямоугольник!

— Верно. Даю 3 минуты, чтобы высчитать периметр этого нового прямоугольника.

Дети принялись за дело. Некоторые думают сами, некоторые объединились по два, по три с сидящими рядом, сзади и впереди детьми, они близко склонили головы друг к другу и шепчутся. Я подзываю к себе Лелу и тоже начинаю шептаться с ней.

— Давай решим задачу вместе, хорошо?

— Хорошо!

— Будем рассуждать так: если прямоугольники приставить большими сторонами, то получим такой прямоугольник, верно? ( Я демонстрирую это с двумя маленькими прямоугольниками, вырезанными из картона. )

— Да!

— Высчитай поскорее, каков будет периметр этого прямоугольника!

Лела считает и допускает ту самую ошибку, которую, думаю, допустят и другие: она слагает длину всех сторон обоих прямоугольников и получает 36 см. Тогда я переворачиваю прямоугольники, с другой стороны указанной длины сторон нет.

— Покажи стороны этого прямоугольника и назови длину каждой!

Девочка сразу соображает.

— Я и те стороны посчитала, которые в середине!

— Но это же новый прямоугольник, значит, их в нем уже не существует!

— Периметр равен 26 см.

— Верно!

Эка ( предупреждает ). Осталось полминуты!

— А теперь, — говорю я Леле, — приставь эти прямоугольники маленькими сторонами и высчитай!

Эка ( объявляет ). Время истекло!

Подхожу к группе в среднем ряду — там объединились Тека, Илико, Вахтанг.

— У нас два ответа: если приставить прямоугольники большими сторонами, то периметр составит 26 см, а если маленькими сторонами, то периметр такого прямоугольника будет равен 28 см! Верно?

Все это говорят мне вместе и Тека, и Илико, и Вахтанг. Вот она, коллективная самостоятельность. Дети возбуждены.

— Верно! — говорю я и улыбаюсь всем троим.

Котэ допустил ту же самую ошибку, что и Лела: он в отдельности высчитал периметры обоих прямоугольников и сложил их, потому и утверждает, что периметр равен 36 см.

— Нет, — говорю мальчику. Рядом с ним сидит Ия. — А ты как думаешь? — спрашиваю девочку.

— Периметр равен 26 см.

— Объясни, пожалуйста, Котэ, как ты получил этот результат.

Мнения в классе расходятся: дети называют и 36 см, и 28 см, и 26 см.

Вызываю к доске группу во главе с Илико.

— Объясните и докажите!

Хотя они говорят наперебой, все же сумели объяснить и доказать и в классе не видно сомневающихся.

— У нас осталось еще одно задание: соединить числа по порядку — от сорока до пятидесяти и от пятидесяти до шестидесяти.

Отодвигаю занавеску на третьей доске.

— Давайте поручим это дело Тее и Елене, вы не против?

Пять-шесть ребятишек, в том числе Тея и Елена, нуждаются в развитии быстрой реакции и сообразительности.

— Задача должна быть решена за минуту! Следите, пожалуйста, насколько правильно они будут действовать! А ты, Марика, смотри на минутную стрелку!